¿Por qué las matemáticas son tan sexis?
En esta brillante charla, que se transcribe a continuación, el afamado y reconocido Matemático francés Cédric Villani (medalla Fields) nos muestra por qué hacer matemáticas resulta tan atractivo y necesario en estos tiempos sumergidos en los datos y sistemas globales. La imaginación y la resolución de problemas sofisticados puede ser tan emocionante y placentera como muchos de los goces convencionales de la vida. Compartido bajo licencia Creative Commons. Todos los derechos Ted Talks. Consulte el video en https://www.ted.com/talks/cedric_villani_what_s_so_sexy_about_math/
Imagen 1. Cédric Villani. Princeton Institute for Advanced Studies
¿Qué hacen los franceses mejor que todos los demás? Si hacemos una encuesta, las tres respuestas podrían ser: el amor, el vino y el lloriqueo. Tal vez, pero permítanme sugerir una cuarta: las matemáticas. ¿Sabían que París tiene más matemáticos que cualquiera otra ciudad del mundo? Además de más calles con nombres de matemáticos. Y si uno mira las estadísticas de la Medalla Fields, a menudo llamada Premio Nobel de matemáticas, y siempre concedida a matemáticos con menos de cuarenta años, verá que Francia tiene más Medallas Fields por habitante que cualquier otro país.
¿Qué nos parece tan atractivo de las matemáticas? Al fin y al cabo, parece que son tediosas y abstractas, con solo números y cálculos y reglas para aplicar. Las matemáticas pueden ser abstractas, pero no son tediosas y no son todo cálculos. Tienen que ver con el raciocinio y con demostrar nuestra principal actividad. Se trata de imaginación, el talento que más apreciamos. Se trata de encontrar la verdad. No hay nada como la sensación que invade a uno cuando tras meses de reflexión, entiende por fin el raciocinio correcto para resolver su problema. El gran matemático André Weil lo comparó, y no es broma, al placer sexual. Pero señaló que ese sentimiento puede durar horas o incluso días.
La recompensa puede ser grande. Verdades matemáticas ocultas están por todas partes en nuestro mundo físico. Son inaccesibles a nuestros sentidos, pero pueden ser vistas a través de lentes matemáticos. Cierren los ojos por un momento y piensen en lo que ocurre ahora a su alrededor. Partículas invisibles del aire chocan con ustedes, miles de millones cada segundo, todo es un completo caos. Y aún así, sus estadísticas pueden ser precisamente previstas por la física matemática. Abran ahora los ojos para las estadísticas de las velocidades de estas partículas.
La famosa curva gaussiana en forma de campana o distribución normal de las desviaciones del comportamiento promedio. Esta curva habla de la estadística de velocidades de las partículas de la misma manera como una curva demográfica hablaría de la estadística de edades de los individuos. Es una de las curvas más importantes. Sigue apareciendo una y otra vez, en muchas teorías y muchos experimentos, como gran ejemplo de universalidad, lo que es tan querido por nosotros los matemáticos.
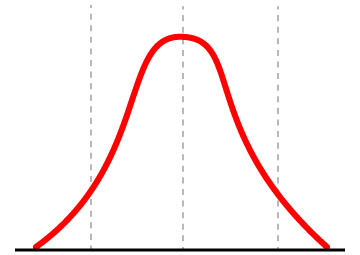
Imagen 2. Curva gaussiana
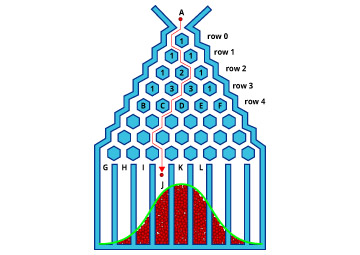
Imagen 3. Tablero de Galton.
Sobre esta curva, el famoso científico Francis Galton dijo: "los griegos la habrían deificado de haberla conocido. Es la ley suprema de la sinrazón". La mejor forma de materializar esa diosa suprema es con el tablero de Galton. Dentro de esta placa hay estrechos túneles a través de la cual diminutas bolas caerán al azar, yendo de derecha a izquierda, o hacia la izquierda, etc. Todo en aleatoriedad y caos completo. Veamos lo que sucede al mirar esas trayectorias aleatorias juntas.
Esto es como un deporte, porque tenemos que resolver algunos atascos de tráfico en ese país. Ajá. Pensamos que la aleatoriedad me jugaría un truco en el escenario. Aquí está. Nuestra diosa suprema de la sinrazón. La curva de Gauss atrapada aquí en esta caja transparente como el sueño en los cómics "The Sandman". Se lo he mostrado así a ustedes, pero a mis estudiantes les explico por qué no podría haber otra curva. Y esto está en contacto con el misterio de esa diosa, sustituyendo una hermosa coincidencia por una hermosa explicación.
Toda la ciencia es así. Y hermosas explicaciones matemáticas no son sólo para nuestro deleite. También cambian nuestra visión del mundo. Por ejemplo, Einstein, Perrin, Smoluchowski, usaron el análisis matemático de las trayectorias aleatorias y la curva de Gauss para explicar y demostrar que nuestro mundo está hecho de átomos. No era la primera vez que la matemática estaba revolucionando nuestra visión del mundo. Hace más de dos mil años, en la época de los antiguos griegos, ya se produjo. En aquellos días, solo una pequeña fracción del mundo había sido explorada, y la Tierra parecería infinita. Pero el inteligente Eratóstenes usando las matemáticas, pudo medir la Tierra con una increíble precisión de 2 %.
He aquí otro ejemplo. En 1673 Jean Richer notó que un péndulo se balancea ligeramente más lento en Cayenne que en París. A partir de esta sola observación y matemáticas inteligentes, Newton dedujo acertadamente que la Tierra es un poquito achatada en los polos, un 0,3 %. tan pequeña que ni siquiera se nota en la visión real de la Tierra. Estas historias muestran que las matemáticas pueden hacernos salir de nuestra intuición, medir la Tierra que parece infinita, ver átomos invisibles o detectar una variación imperceptible de forma. Y si solo hay una cosa que ustedes pueden aprovechar de esta charla, es la siguiente: las matemáticas nos permiten ir más allá de la intuición y explorar territorios que no están a nuestro alcance.
Esto es un ejemplo moderno para todos ustedes. Se refieren a buscar en nternet. La World Wide Web, más de mil millones de páginas web, ¿Quieren repasar todas ellas? La potencia informática ayuda, pero sin el modelado matemático ésta sería inútil para encontrar la información oculta en los datos. Vamos a resolver un problema hiper fácil. Imagine que usted es un detective trabajando en un caso penal, y hay muchas personas con su versión de los hechos. ¿A quién entrevistaría primero? Respuesta sensata: a los testigos principales.
Vean, supongamos que la persona número siete, cuenta una historia, pero cuando se le pregunta de dónde sacó la historia, apunta a la persona número tres como fuente. Y la persona número tres, a su vez, apunta a la persona número uno como fuente primaria. Ahora el número uno es el principal testigo, así que definitivamente quiero entrevistarlo con prioridad. Y a partir de la gráfica también vemos que la persona número cuatro es un testigo principal. Y puede que incluso quiera entrevistarlo en primer lugar, porque hay varias personas que se refieren a él.
Bien, eso fue fácil. Pero ahora ¿qué pasa si un gran grupo de personas va a declarar? Y este grafo, puedo pensarlo como todas las personas que atestiguan en un caso de delito complicado. Pero pueden muy bien ser páginas web apuntando uno al otro, refiriéndose a la otra para los contenidos. ¿Cuáles son las más autorizadas? No es tan claro.
