El desarrollo de la computación cuántica aún es experimental, y representa muchísimos desafíos tecnológicos el poder llegar a construir las computadoras cuánticas. En este artículo se pretende explicar qué es la computación cuántica al compararla brevemente con la computación clásica, e introducirnos a lo que es y cómo funciona la mecánica cuántica, que es la forma en que operarían estas computadoras cuánticas. .
Introducción
Para poder entender qué es la computación cuántica, deberemos entender qué es la computación clásica. Desde que se concibió la computación con la Máquina de Babbage, aunque esta quedó en el diseño solamente, nos sentó las bases para crear las primeras computadoras que usan solo 0 y 1 para realizar sus operaciones, los bits o binarias, pasando por la historia desde la computadora Z3 de los nazis, la ENIAC de EUA en 1946, las VAX en los 70, las mini y microcomputadoras, la supercomputadora, la Cray de los 80, por mencionar algunas, y hasta nuestras fechas con los teléfonos inteligentes y la computación de alto rendimiento, por diferentes tecnologías que van desde la primera válvula electrónica (bulbo), el transistor y ahora los circuitos integrados, la computación y la informática no solo se definen en sus componentes electrónicos (hardware), también se definen por la programación (software).
Una de las características de las computadoras actuales que aún no ha cambiado es el uso de la electrónica y la forma en que se programan.
Desde el punto de vista de la teoría de la computación nuestras computadoras actuales son llamadas máquinas de estados finitos, es decir, tienen una sola entrada y una sola salida, y son secuenciales a lo cual llamamos programación secuencial.
El diseño de los programas es una serie de instrucciones en código binario que se ingresan a la computadora de manera secuencial, se conocen como algoritmos.
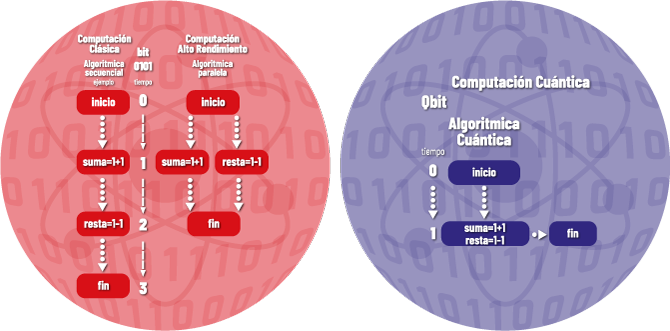
Figura 1. Infografía comparativa de la computación clásica y la cuántica.
De izquierda a derecha, se muestran 3 algoritmos con la misma escala de tiempo, representados por un diagrama de flujo donde se observan 2 operaciones aritméticas, una suma y una resta.
En el de la izquierda se muestra la suma en el tiempo 1 y la resta en el tiempo 2. En el de en medio se muestra que la suma y la resta se hacen en forma paralela en el tiempo 1.
En el de la derecha se muestra como se representa el cálculo mediante cómputo cuántico donde dos o más operaciones se pueden realizar en un tiempo menor a 1.
Como observamos en la Figura 1, las operaciones secuenciales significan que es sucesivo y en un orden específico, pero, si esto sucede en la computación clásica, ¿cómo es que parece que los programas se ejecutan de manera inmediata?
La realidad es que gracias a la tecnología electrónica (hardware más eficiente) estos procesos secuenciales se realizan tan rápido que en nuestro tiempo de referencia parece que se realizan al mismo tiempo, sin embargo la ejecución de los procesos es secuencial, aunque sea muy rápido, esto implica que siempre se requiere una unidad de tiempo para ejecutarse, por esta razón hay problemas de cálculo numérico y simulaciones en los cuales el cómputo clásico y el cómputo de alto rendimiento no pueden acabar las operaciones en tiempos útiles o más bien se consideraron interminables, un ejemplo de esto es el cálculo del genoma humano, la predicción de terremotos, el clima de todo un año, etc.
Cuando inició la computación clásica, las operaciones se medían por miles o millones de operaciones por segundo, ahora las operaciones son tan rápidas que se usan términos como operaciones de punto flotante o flops y de hecho en una forma más general nos referimos a la velocidad de las computadoras en la frecuencia operan los procesadores.
Cuando nos referimos a un procesador es en realidad hablamos de una cápsula de silicio que tiene en su interior millones de transistores enlazados, los cuales tienen entradas y salidas para poder realizar las operaciones las cuales son más rápidas dependiendo de la cantidad de transistores que tengan, por lo cual nos referimos a que entre más número de transistores en la cápsula de silicio, más rápida será la computadora.
En este respecto en 1975 Gordon Moore perfecciona una ley, en donde la rapidez de los procesadores la relaciona de manera proporcional con el tamaño físico, y, en la actualidad los procesadores tienen transistores de tamaños nanoscópicos, es decir , esto es una millonésima parte de un metro, y para comprender esta dimensión significa que son del tamaño de una partícula subatómica como el fotón.
¿Es posible realizar cálculos cada vez más rápido?
Para el caso de la Ley de Moore, el límite es el Atómico, es decir no podemos diseñar transistores del tamaño del átomo.
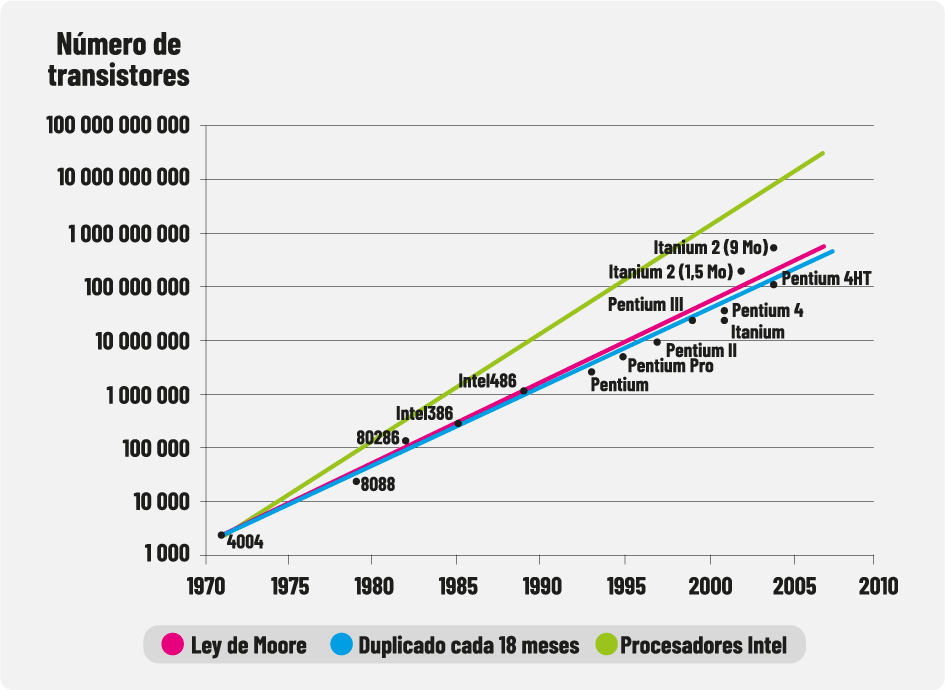
Figura 2. Wikipedia, Ley de Moore hasta el 2010. En el gráfico de cada 5 años y millones de transistores se explica la observación de Moore donde cada 5 años hay cada vez más transistores en el procesador desarrollado en el año indicado
Por lo cual y desde 1981 Paul Benioff establece los principios del cómputo cuántico, y varios matemáticos desarrollaron teorías al respecto, refiriéndose a que la interacción de partículas subatómicas podrían servir para realizar cálculos numéricos, con muchísima más rapidez, entonces mencionamos a Peter Shor quien ya incursionó en el desarrollo de algoritmos cuánticos e incluso David Deutsch que sigue en el desarrollo de algoritmos cuánticos.
Entonces, para entender la computación cuántica necesitamos primero entender qué es la Mecánica Cuántica.
La mecánica cuántica es la rama de la física que estudia la naturaleza y la interacción de las partículas atómicas y subatómicas.
Un ejemplo característico de la mecánica cuántica es la dualidad onda partícula de la luz. Christiaan Huygens consideraba que la luz era una onda y Sir. Isacc Newton una partícula, y ambos tienen razón la luz tiene una dualidad es onda y al mismo tiempo partícula.
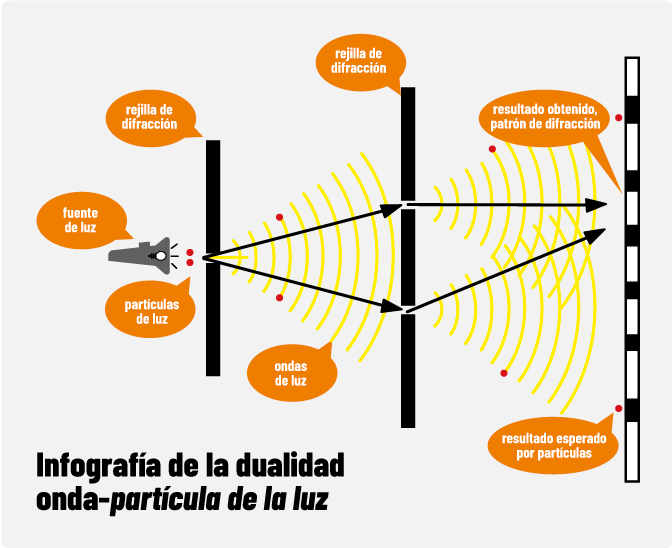
Figura 2.1 Explicación de la dualidad onda-partícula, a partir de una fuente de luz, se observa cómo viajan las ondas y las partículas, sin embargo al llegar a su destino después de pasar por pequeñísimas agujeros llamados rejillas de difracción, la luz se comporta como onda y se muestra en el patrón de difracción, el cual muestra zonas claras y zonas oscuras debido a la interferencia de las mismas ondas, oscuras cuando se interfieren y claras cuando se suman entre sí. Sin embargo, si no fueran ondas se comportarían como los puntos que representan una partícula, que aparecen en donde solo un par de ellos logran pasar hasta llegar al final.
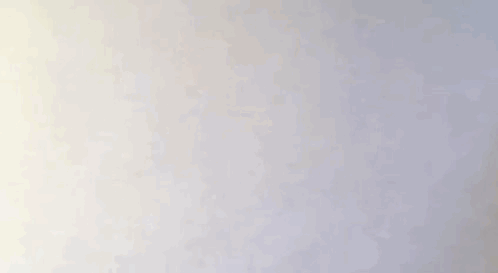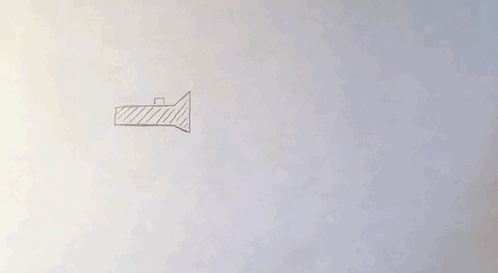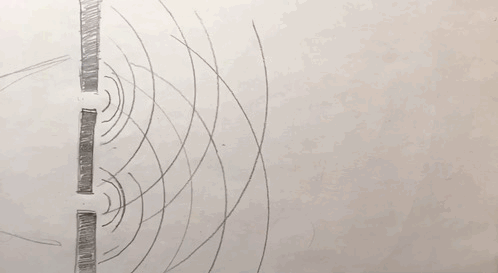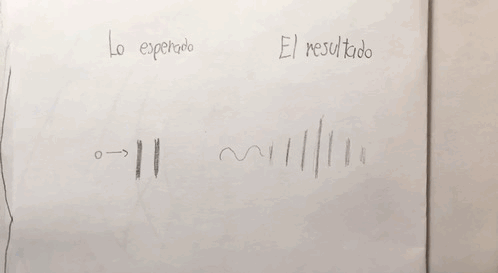
Figura 2.2 Animación de la dualidad onda-partícula de la luz (Cortesia Demian Ruiz) http://triton.astroscu.unam.mx/fruiz/video/Onda_Particula.GIF
¿Y cómo es que la luz es una onda y una partícula al mismo tiempo?
Esto lo explicamos con el desarrollo de la mecánica cuántica la cual comprobó que las partículas subatómicas, incluida la luz, tienen propiedades de onda y de partícula. Erwin Schrödinger en 1935 establece la paradoja del gato de Schrödinger, indica que no podemostener la certeza de si un gato encerrado en una caja hermética, está vivo o muerto. Es como si lanzamos una moneda al aire, mientras esté girando es a la vez águila o sol, no sabremos con qué cara caerá hasta que se detiene.

Figura 3. Wikipedia Explicación del experimento conceptual de la paradoja del “gato de Schrödinger” En el experimento que imaginó Schrödinger, el gato podría estar vivo o muerto debido a que existe un dispositivo que si detecta una partícula, o que alguien observa lo que hay dentro de la caja se libera un veneno que mataría al gato de manera inmediata.
Es decir que mientras no hagamos las observaciones, el gato podría estar vivo o muerto al mismo tiempo.
Si abrimos la caja estará siempre muerto, ya sea que estaba muerto desde antes de que abriéramos la caja o por el hecho de abrirla. Con esta paradoja Schrödinger explica cómo se comportan las partículas en el mundo subatómico de la mecánica cuántica.
Otra forma de explicarlo es con uno de los grandes inventos del siglo XX, y producto del estudio de la mecánica cuántica: la luz láser. Los estudios de la radiación o luz láser “rayo láser”, fueron realizados en los años 60 y 70. La palabra láser proviene del acrónimo LASER del inglés: “Light Amplification by Stimulated Emission of Radiation”, que traducido al español es amplificación de la luz por emisión estimulada de radiación.
Albert Einstein descubrió que los átomos en resonancia son capaces de producir partículas (fotones) en el mismo estado, es decir duplicar su estado, lo que implica que los fotones son idénticos. Esta propiedad se conoce como entrelazamiento cuántico, y se logra fácilmente con el láser mediante espejos paralelos al haz de emisión con una distancia que es múltiplo de la longitud de onda. Los fotones de igual cantidad de energía y radiación producen un láser.
Einstein predijo teóricamente antes de la invención del láser que la probabilidad de duplicar el estado de un fotón o cualquier partícula subatómica es a partir de entrelazado cuántico.
Para comprender la resonancia o entrelazado cuántico se puede comparar con la resonancia auditiva, por ejemplo, un diapasón el cual lo hacemos sonar en una guitarra, únicamente hará vibrar la nota que corresponde a la cuerda de la guitarra, esto con el fin de afinarla; es decir cuando la cuerda vibra cuando corresponde a la nota del diapasón esto le llamamos resonancia.
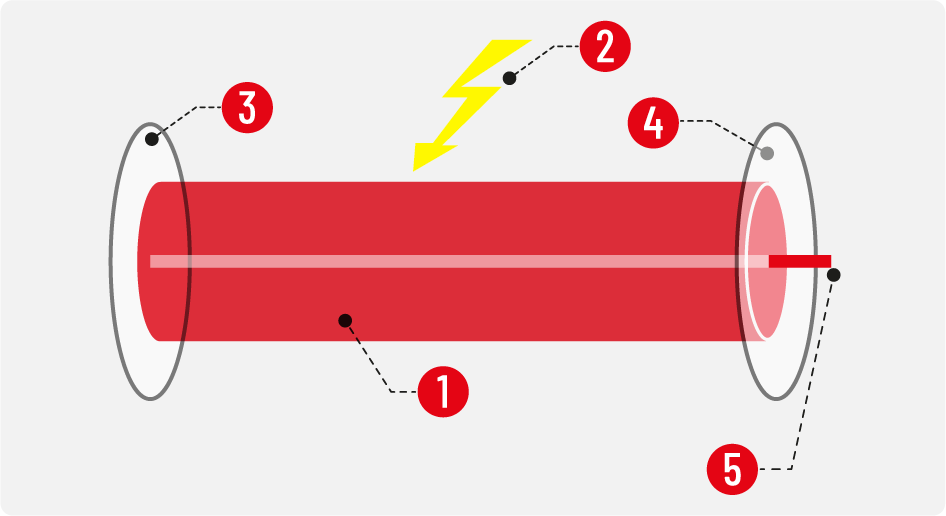
Figura 4. Wikipedia, Cavidad resonante de un láser, 1. Medio activo con ganancia óptica 2. Energía de bombeo para el láser 3. Espejo de alta reflectancia 4. Espejo semi-transparente (permite la salida de luz láser) 5. Emisión del haz láser.
Lo mismo pasa cuando un electrón pasa de un nivel de energía a otro y se produce un fotón que está cuantizado. Es decir, los niveles de energía de los átomos son valores fijos y discretos.
¿Pero todo esto es para entender el cómputo cuántico?
Sí, y de hecho para explicar esa parte de resonancia, la operación de las computadoras cuánticas se realiza mediante la resonancia cuántica. Y aquí en lugar de tener bits, como los tenemos en las computadoras clásicas, la nueva unidad utilizada es qubit, “cubit” o bit cuántico, el qubit es el que determina el estado encendido o apagado de una computadora cuántica, por lo cual requerimos resonancias para manipular el estado de 0 o 1 qubit.
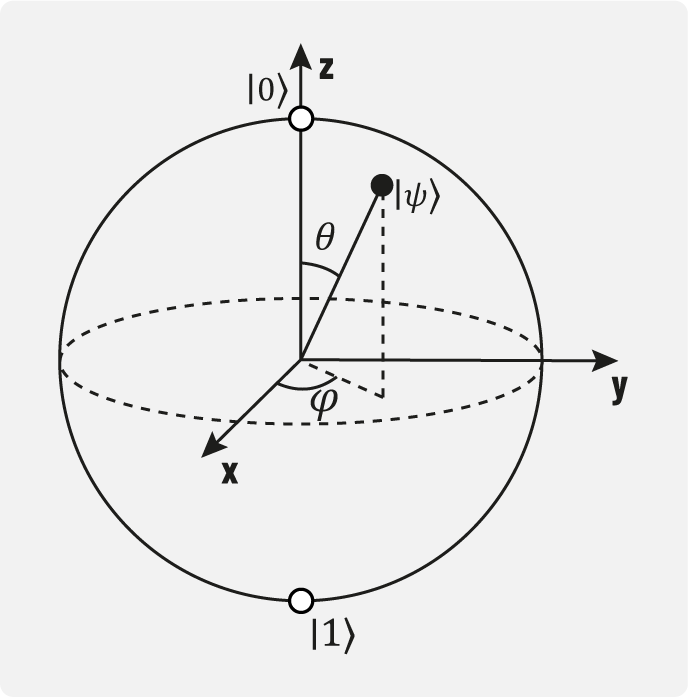
Figura 5. Wikipedia Representación gráfica de un cúbit en forma de esfera de Bloch: aparte de los estados llamados { | 0 ⟩ , | 1 ⟩ }, son posibles estados generales de tipo | Ψ ⟩
La esfera de Bloch es una representación geométrica del espacio de estados puros de un sistema cuántico de dos niveles, usado para obtener los qubits
Los estados { | 0 ⟩ , | 1 ⟩ } y | Ψ ⟩ son la representación matemática del estado de las partículas, acerca de las cuales físicamente no es posible saber el estado en el que se encuentran en un momento dado.
De hecho, va más allá de producir un qubit, puesto que debido a los estados de las partículas, es posible tener 255 qubits, en el mismo tiempo que se tiene un 0 o 1 bits.
Por esta razón una computadora cuántica tiene muchas entradas y muchas salidas, por lo tanto es necesario establecer un método para poder escoger las salidas que corresponden a los resultados correctos, y en este sentido Peter Shor elaboró un método matemático que resuelve este problema y a este método lo conocemos como el Algoritmo de Shor, el cual consiste en descomponer en factores todas estas salidas en un tiempo determinado.
Existen muchos métodos (algoritmos) para la computación cuántica, el de Shor es el más utilizado, pero podemos mencionar más como: Algoritmo Deutsch-Jozsa (1992), Algoritmo de Shor (1995), Algoritmo de Grover (1996) https://quantumalgorithmzoo.org/
La forma de obtener el qubit se explica en la Figura 5 y es la posición en la que se encuentra la partícula subatómica según descrito en el diagrama de Bloch, como según vimos en la paradoja de Schrödinger en la Figura 3, la partícula tendrá 2 estados al mismo tiempo, por lo cual tenemos 0 y 1 al mismo tiempo, entonces por medio de resonancia podremos manipular el estado que queremos que tenga, y de esa manera podremos obtener un qubit 0 o un qubit 1.
La única forma de poder manipular partículas subatómicas hasta nuestros días es por medio de superconductores, y recientemente por medio de luz láser.
En la siguiente figura (figura 6) se muestra el diseño de un procesador cuántico el cual mediante entrelazamiento cuántico de luz láser, se puede observar el diseño de la condicionan los estados de la luz para obtener un qubit el cual no da el resultado de 1 o 0 dependiendo el estado de la luz que se obtiene mediante el Algoritmo de Shor.
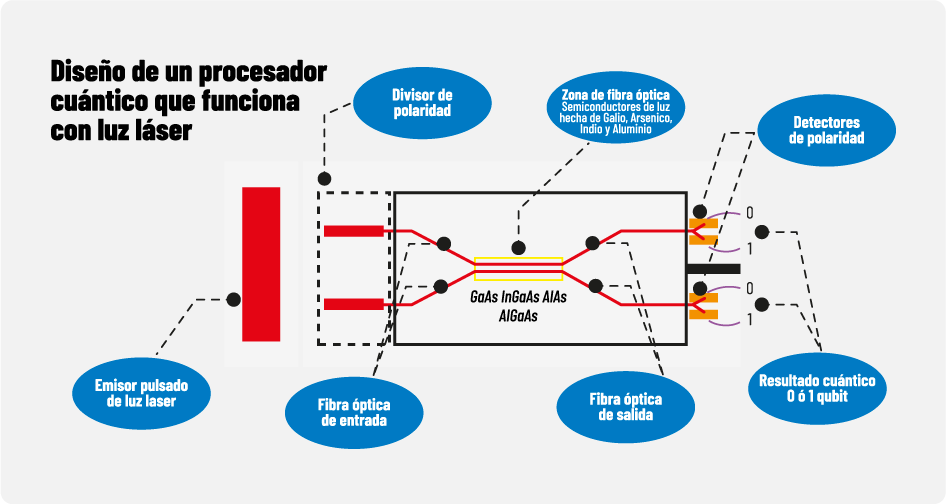
Figura 6. Diseño de un procesador cuántico en el cual por medio de un emisor de luz láser, se envían por dos caminos diferentes de fibra óptica al mismo tiempo la luz láser con polaridad diferente, al pasar por la zona semiconductora de en medio en la cual la Fibra Óptica Semiconductores se junta (marcada con amarillo), esta zona está hecha de los elementos Galio(Ga) Arsénico(As) Indio(In) y Aluminio(Al), los cuales combinados, forman un estado semiconductor óptico en el cual la luz continuará su camino solo por una y solo una de las fibras ópticas de salida, y allí se contabilizará un solo qubit con una sola polaridad en cualquiera de los detectores.
El cómputo cuántico utiliza el entrelazamiento cuántico como herramienta para manipular las partículas subatómicas y poderlas utilizar como qubits, los cuales realizan operaciones matemáticas, por medio del algoritmo de Shor como se explicó anteriormente.
Lo que se quiere hacer en la computación cuántica es realizar operaciones más rápidas, lo cual sí es posible pero los algoritmos secuenciales que conocemos en la computación clásica no son válidos para la computación cuántica, como se muestra en la figura 1.
¿Una computadora cuántica funcionaría como nuestras computadoras convencionales?
La respuesta es NO, según la “teoría de la computación”, la computadora clásicase define como una máquina de estados finitos, una entrada y una salida.
En contraste una computadora cuántica según esta misma teoría son múltiples entradas y múltiples salidas al mismo tiempo, es decir estados infinitos, por lo cual no sabemos los cuales son los resultados correctos, es decir, y tomando como ejemplo la paradoja de Schrödinger, queremos vivo al gato pero no sabemos si lo veremos vivo o muerto (Figura 3 “Gato de Schrödinger”).
Es muy importante mencionar que para poder operar una computadora cuántica necesitamos una computadora clásica que nos ayude a recabar y almacenar los resultados.
De hecho compañías como IBM, HP, Google, han diseñado lenguajes especiales para simular la programación cuántica, como son Qiskit de IBM, Google Quantum AI, Microsoft Azure Quantum, en donde por medio de algoritmos cuánticos con simuladores en lenguaje como Python, F, Visual Studio Code, como interfaz, se simulan algoritmos básicos de programación cuántica.
Pues entendiendo lo que llamamos en este texto como computación clásica, es la que todos usamos día a día, encontramos 3 diferencias fundamentales con la computación cuántica:
Computación clásica
1.- La computación clásica es secuencial.
2.- La computación clásica se programa con algoritmos secuenciales (ver Figura 1 Izquierda y en medio).
3.- La computación clásica se usa con electrónica como hardware la cual ya es nanométrica.
4.- La Teoría de la Computación nos define la computación clásica como una máquina de estados finitos una entrada, una salida en una unidad de tiempo.
Computación cuántica:
1.- La computación cuántica no es secuencial (ver Figura 1 derecha)
2.- Se programa con algoritmos que no son secuenciales como lo describen algoritmos cuánticos como el de Shor
3.- El hardware de la computación cuántica es con superconductores y/o luz láser para manipular partículas subatómicas.
4.- La Teoría de la Computación nos define la computación cuántica como una máquina de estados infinitos muchas entradas, muchas salidas en una unidad de tiempo. Una forma de entenderlo es con este video de la University of Sheffield:
Conclusiones
La computación cuántica apenas comienza, tanto en su software (programación y su algoritmia) como en su hardware (equipos de manipulación subatómica) y cambia totalmente, por ejemplo en su programación no es secuencial, y por tanto, es necesario reelaborar todos los problemas resueltos por las computadoras clásicas, y esto representa un gran reto.
Las compañías están invirtiendo en la elaboración de equipos que puedan hacer operaciones por medio de cómputo cuántico, y se han resuelto algunos problemas por medio de computación cuántica, pero faltan grandes problemas por resolver que se han presentado como grandes retos en la computación clásica.
Por ejemplo en el caso de seguridad en cómputo, la computación clásica tardaría en descifrar una contraseña de 10 caracteres (con mayúsculas minúsculas y caracteres especiales) un tiempo aproximado de 5 años, pero se espera que con la computación cuántica este proceso tarde tan solo unos minutos, esto implicaría que nuestras contraseñas de cuentas de banco, correos, redes sociales, teléfonos, etc. ya no serían seguras puesto que podrían descifrarlos por medio de la computación cuántica en unos cuantos minutos.
Sin embargo, no tenemos por qué preocuparnos, debido a que si existen las computadoras cuánticas, también nos ayudarían para protegernos, y se generarían programas cuánticos de protección que nos permitan eliminar esta vulnerabilidad en las contraseñas.
Otro gran reto es el poder predecir grandes terremotos que afectan las grandes ciudades, y de esta manera poder evitar muertes y destrucción.
Referencias:
Aaronson, S. (8 de junio de 2021). What makes quantum computing so hard to explain?, en Quanta Magazine. https://www.quantamagazine.org/why-is-quantum-computing-so-hard-to-explain-20210608/
Giles, M. (29 de enero de 2019). Explainer: What is a quantum computer?
How it works, why it’s so powerful, and where it’s likely to be most useful first, en MIT Technology Review. https://www.technologyreview.com/2019/01/29/66141/what-is-quantum-computing/
Hagar, A. y Cuffaro, M. (30 de diciembre de 2019). Quantum Computing, en Stanford Encyclopedia of Philosophy., Edición de Otoño de 2022. https://plato.stanford.edu/entries/qt-quantcomp/
Hernampérez, R. (23 de noviembre de 2022). Introducción a la computación cuántica. Blog En mi local funciona. https://www.enmilocalfunciona.io/introduccion-a-la-computacion-cuantica/
Ivanov, T. (2020). Computación cuántica: introducción al paradigma cuántico universal, situación actual, herramientas de desarrollo, estudio e implementación del algoritmo Quantum Counting clásico, desarrollo de una versión simplificada del algoritmo y aplicaciones prácticas. Trabajo de grado de Ingeniería de computadores. Universidad Politécnica de Madrid. https://oa.upm.es/64931/1/TFG_TODOR_KRASIMIRO_IVANOV.pdf
Jordan, S. y colaboradores en línea (2023). Algebraic and Number Theoretic Algorithms. National Institute of Standards and Technology y Quantum Algorithm Zoo. https://quantumalgorithmzoo.org/
Lu, D. (28 de octubre de 2019 ). What is a quantum computer? The technology harnesses quantum physics to perform calculations faster than ever, en New Scientist. https://www.newscientist.com/question/what-is-a-quantum-computer/
Mayo Infografía (10 de enero de 2020). ¿Qué es la Computación Cuántica? https://mayoinfografia.com/que-es-la-computacion-cuantica/
Politi, A.,Matthews, J. y O’Brien, J. (4 de septiembre de 2009), Shor’s Quantum Factoring Algorithm on a Photonic Chip, en Science 325: 1221, https://www.science.org/doi/10.1126/science.1173731
Rolando Saniz, R. (2001). Computación cuántica, en Revista Acta Nova. v.1 n.2 http://www.scielo.org.bo/scielo.php?script=sci_arttext&pid=S1683-07892001000200006
Quantum animations (2015). Circuito Cuántico Computacional usando luz en un chip. Quantum Light University of Sheffield. https://www.youtube.com/watch?v=nyK-vhoOBpE
Ficha del autor
L.I. Francisco Ruiz Sala: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Licenciado en informática y especialista en Cómputo de Alto Rendimiento por el Instituto de Matemáticas Aplicadas en Sistemas (IIMAS) de la UNAM. Profesor de Asignatura de la Facultad de Ciencias UNAM, en la materia de Computación y maestrante en Ingeniería y Ciencias de la Computación en la UNAM. Actualmente Académico adscrito al Departamento de Cómputo en el Instituto de Astronomía de la UNAM.



