
Cada vez son más frecuentes las apariciones de la inteligencia Artificial (IA) en la vida moderna. ¿Cuáles son sus conceptos y fundamentos? ¿Es posible que las máquinas aprendan? En este artículo haremos un modelo de inteligencia artificial que aprende y mejora sin necesidad de una computadora.
En los últimos años se escuchan cada vez con mayor frecuencia los términos inteligencia artificial y aprendizaje de máquina, ambos relacionados con las ciencias de la computación. La inteligencia artificial actualmente se aplica en áreas muy diversas: los coches autónomos, los asistentes digitales en teléfonos y computadoras, las compras online, la agricultura inteligente, las búsquedas web, las aplicaciones de traducción, la ciberseguridad, los robots, la manufactura, el diseño y la optimización, etc. Stephen Hawking dijo que cada aspecto de nuestras vidas será transformado por la IA y que ésta podría ser el evento más importante en la historia de nuestra civilización.
Muchos de los algoritmos para la IA se forman a partir de una estructura de datos con un conjunto de características especiales llamada Red Neuronal. Una red neuronal consiste en varios niveles o columnas que presentan un arreglo de “neuronas” o nodos. En cada nivel o columna hay un número determinado de neuronas. Cada neurona de cada nivel tendrá una conexión con todas las neuronas del siguiente nivel y dicha conexión tendrá un peso, es decir, un valor numérico inicialmente arbitrario. Por ejemplo:
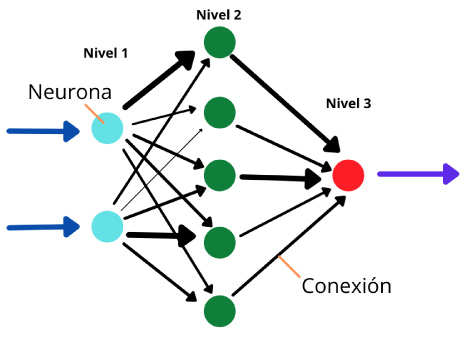
Figura 1. Algoritmos para la Inteligencia Artificial
El concepto de red neuronal se ha desarrollado de la mano del desarrollo de la inteligencia artificial y se asocia a una representación abstracta de los sistemas neuronales en la naturaleza. Incluso se han podido estudiar redes neuronales de complejidades variables en el cuerpo humano. Así, por ejemplo, existe una red neuronal en el fondo de la retina del ojo cuya función es discriminar qué información será conducida y cuál filtrada al nervio óptico. Esto permite no sobrecargar el cerebro, al cual le es fácil recrear o rellenar toda la información necesaria para tener una imagen cerebral “completa” de lo que se observa.
Las redes neuronales contienen en la definición de su estructura una condición dinámica que se puede modificar mientras más se va usando y que va “aprendiendo” dependiendo de los resultados esperados.
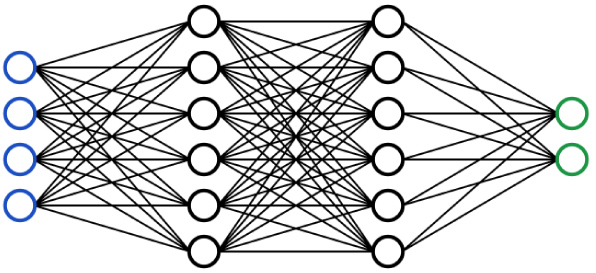
Figura 2. Redes Neuronales
Un ejemplo famoso es el uso de redes neuronales para hacer reconocimiento de imágenes. Si tenemos un conjunto muy grande de fotos de gatos y otros animales y tenemos una etiqueta que diga cuál es el animal en cuestión, podemos crear una red neuronal que empiece en la imagen y termine en dos neuronas que representan si algo es gato o no. Al sistema se le presenta la primera foto y se asignan valores aleatorios en cada una de sus conexiones. Si el resultado casualmente dice que es gato y la foto lo era, todas las conexiones que llevaron a este resultado se premian y aumentan.
Por lo contrario, cuando la red se “equivoca” y no acierta, se disminuyen todos los “pesos” de las conexiones que derivaron en dicho resultado fallido. Después de presentar una cantidad muy grande de fotos, donde pudimos premiar o castigar los resultados del reconocimiento, la red empezará a acertar cada vez con mayor precisión, hasta llegar a niveles sorprendentes.
Fabricaremos, pues, una red neuronal y practicaremos el concepto de “aprendizaje de máquina” mediante un ejercicio que se puede reproducir fácilmente en clase y sin necesidad de una computadora. Pero antes veremos cómo se llegó a este sistema que ensayaremos.
Figura 3. Donald Michie
Durante la Segunda Guerra Mundial algunas de las mentes británicas más brillantes que trabajaban en la criptografía de mensajes enviados por el bando enemigo, obtuvieron un entrenamiento notable en la interpretación de códigos complejos. Uno de ellos fue Donald Michie, quien en 1961 construyó, como una prueba frente a los escépticos, un modelo físico sin computadora (en esos años no era fácil contar con una computadora digital) que pudiera aprender, mejorar y hasta ganar un juego de Gato (Tic tac toe). Lo llamó MENACE.

Figura 4. Programa MENACE
El sistema consiste en una colección de cajas de cerillos. Cada caja corresponde a un posible estado del juego. Cada estado contiene unas cuantas jugadas posibles para el “programa”. Dentro de la caja hay tantas fichas como jugadas posibles, a partir de ese estado. Cada opción corresponde a un color predeterminado sobre la casilla de dicha jugada. Se saca una ficha al azar y esa es la jugada de la máquina. Cuando la partida llega a su fin, si la máquina pierde, no se volverán a introducir las fichas en sus cajitas correspondientes. Si el juego llega a empate, se pondrá por cada ficha extraída una ficha más de ese color. Y si lo ganó la máquina, se introducirán 3 fichas más del mismo color extraído.
El ejercicio consistía en jugar repetidas partidas contra el programa para entrenarlo. Después de varios juegos el sistema habrá perdido las fichas que correspondían a las jugadas que la hicieran perder. Es decir, aprendió a jugar para ganar o empatar en el peor de los casos.

Figura 5. Martin Gardner
En el siglo XX en Estados Unidos el famoso escritor de la columna de matemáticas recreativas en la Revista Scientific American, Martin Gardner, inventó un mini-juego basado en el ajedrez, llamado Hexapawn. El objetivo era demostrar el aprendizaje de máquina con un sistema más pequeño que MENACE. Además, buscaba un juego que tuviera una solución, de manera que si se juega de una forma precisa, el triunfo está garantizado.

Figura 6. Juego Hexapawn
Hexapawn consiste en un tablero de 3 X 3 casillas y 3 fichas para cada uno de los dos jugadores: un ser humano y la máquina. Las piezas son como los peones del ajedrez, caminan hacia adelante una casilla por vez y si nada lo impide. Pueden avanzar una casilla en diagonal si existe un peón enemigo en la casilla de enfrente, comiéndoselo al avanzar. El propósito del juego es llevar a un peón al extremo opuesto del tablero. También se gana la partida si el contrincante no puede avanzar por tener bloqueadas las casillas hacia el frente de cada uno de sus peones.
El árbol de estados en que puede estar este juego es mucho menor a MENACE, sólo son posibles 24 situaciones o estados:
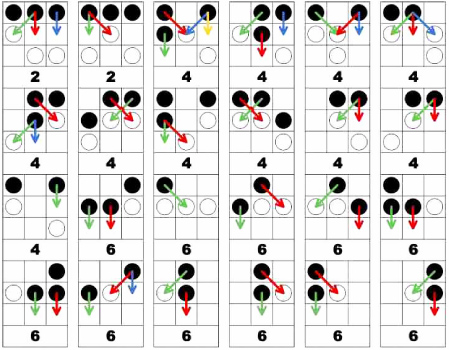
Figura 7. Árbol de estados de Hexapawn
En el turno 1 empieza jugando el humano. En el turno dos sólo hay dos estados posibles. En el turno 4 hay 11 posibles movimientos de la máquina y en el último turno, el sexto, hay de nuevo 11 posibilidades.
Cada etiqueta deberá ir pegada a cada caja de cerillos (sin cerillos) y con una ficha correspondiente a las diferentes flechas dibujadas en las etiquetas. Cuando al sistema le toque elegir cuál será su movimiento se deberá tomar aleatoriamente una de las fichas de la cajita del estado en cuestión. Y dependiendo del color de la ficha extraída se hará la jugada visualizada por la flecha del color correspondiente en la etiqueta.

Figura 8. Cajas de los estados de cada partida
Las cajas de los estados considerados en cada partida se mantienen aparte hasta el final de la partida y también la ficha extraída en cada turno.
Si la partida se pierde, no se vuelve a reintroducir las fichas sacadas en todos los turnos de todas las cajitas usadas. En caso de ser empate, se reintroduce la ficha junto con otra del mismo color en las cajas correspondientes. Y si se gana, se reintroduce la ficha de cada turno junto con otras dos del mismo color.
Estas acciones son el modo en que el sistema premia las jugadas que lo llevan a ganar (agregar dos fichas más de ese color aumenta las probabilidades de que en partidas subsiguientes esa jugada se repita). En caso de haber empate se agregó una más de la ficha seleccionada y en caso de haber perdido la partida el sistema se “autocastiga” eliminando la jugada que lo llevó perder. El castigo es la acción frente al error y el premio es el reforzamiento de los aciertos.
¿Qué es la inteligencia?, ¿qué es el aprendizaje?, ¿qué sistemas nos permiten instrumentar el modo en que la naturaleza procesa la información? Una estructura de información puede implicar un gran poder de procesamiento en sí. Explorar estos temas y hacer esta práctica con los alumnos tiene múltiples beneficios interesantes relacionados con el estudio de las matemáticas, las ciencias de la computación, la filosofía, las ciencias de la cognición, la ingeniería y múltiples áreas en los diferentes ámbitos de uso de la Inteligencia Artificial.
- Un popular video de Ciencia que explica este sistema está en el siguiente link: The Game That Learns (https://www.youtube.com/watch?v=sw7UAZNgGg8)
Referencias
Gardner, M. (1962). How to build a game-learning machine and then teach it to play and to win. Mathematical Games. Scientific American 206 (3). http://cs.williams.edu/~freund/cs136-073/GardnerHexapawn.pdf
Kennedy, J., Eberhart, R. C., Shi, Y. (2001). Swarm Intelligence. Academic Press. https://books.google.com/books?id=Z1z3byh1JAsC&pg=PA137
Michie, D. (2013). BOXES: An experiment in adaptive control. University of Edinburgh. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.474.2430&rep=rep1&type=pdf
Vsauce2. (18 de marzo de 2019). The Game that learns [archivo de video]. https://www.youtube.com/watch?v=sw7UAZNgGg8
Wylie, C. (2018). The History of Neural Networks and AI: Part II. Open Data Science - Your News Source for AI, Machine Learning & more. https://opendatascience.com/the-history-of-neural-networks-and-ai-part-ii/
Ficha del autor
Luis Leñero Elu: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Estudió Matemáticas en la Facultad de Ciencias de la UNAM. Es compositor, maestro y fundador del Instituto del Juego. Se ha dedicado a la enseñanza y la comunicación educativa aplicando tecnologías y gamificación en diversos ámbitos.



