
Albert Einstein
Los principales retos en la enseñanza de las matemáticas radican en la batalla constante contra los prejuicios que existen frente a cualquier tema que asocien los estudiantes con esta disciplina. A menudo los maestros nos enfrentamos a traumas históricos que se acrecientan con el paso del tiempo en la mente de los estudiantes. Muchos de estos traumas se deben al uso de estrategias emocionalmente delicadas, como es la de favorecer la competitividad o dejar en evidencia a aquellos a quienes les cuesta más esfuerzo comprender. La posibilidad de subsanar esta predisposición descansa en la capacidad de los maestros para contagiar su entusiasmo por las Matemáticas y su aprendizaje. La narración y actualización situacional es un elemento clave para crear vínculos positivos con los alumnos y despertar su interés en la materia. "El poder de la imaginación" va dirigido a la comprensión de la fuerza, simpleza y alcance de esta función cognitiva no siempre asociada a la disciplina de las Matemáticas, pero indiscutiblemente útil en esta área del conocimiento.
Se levanta temprano y percibe una cálida brisa marina que inunda su habitación. Más tarde, cuando el Sol empieza a subir, sentado en su escritorio escribe apenas un poco de su libro en desarrollo, pero no logra concentrarse: ansía que pase pronto la mañana y llegue el esperado mediodía. Prepara sus cosas dentro su bolsa de cuero. Lleva sus instrumentos, unos folios de papel papiro, tiza y un bastón largo, justo de un beuma de longitud, equivalente a poco más de metro y medio. Mientras camina hacia el pozo, sus sandalias acompasan rítmicamente a su pensamiento. Poco a poco un esquema y una lógica se materializan y se trazan en su mente: "Sombras iguales: Tierra plana. Sombras diferentes: Tierra esférica. ¿Qué tan diferentes? Poco diferentes: Tierra enorme. Muy diferentes: Tierra pequeña. ¿Qué tan grande es?" En su mente sorprendente de Alfa y no de Beta, como sus envidiosos críticos le llaman, dibuja en aquel gran espacio interior una superficie curva, y sobre ella, dos enormes torres de igual altura. Esa superficie es la superficie del planeta. Toda la Tierra se encuentra ahí dentro, en su cabeza.
Imagina ese gran mapa que tanto amaba ver. Imagina ese mapa curvo. Cada torre se levanta en dos ciudades: Alejandría y Siena. Ambas en Egipto (Siena es ahora Asuán). Recuerda aquel día extraño en el que descubrió esa referencia marginal, una anécdota casi insignificante, una simple peculiaridad. En Siena, durante el solsticio de verano y precisamente a mediodía, sucedía que en el más profundo y siempre oscuro pozo se reflejaba aquel que se asomara metros arriba. Dato curioso, pensó al paso. Pero aquella curiosidad insistente y penetrante no tardó en dominar su mente como un mosquito molesto que lo hacía desconcentrarse a toda hora.
Días más tarde, su pensamiento jugaba con esquemas del Sol, la Tierra, los rayos de luz en los que se asomaban líneas, curvas, superficies y ángulos. En aquella sencillez conceptual solo habitaba lo importante; los detalles particulares, todo lo que sabía de la realidad, de la naturaleza y de los planetas se borraba mágicamente. Entraba al poderoso mundo de la imaginación geométrica. Ahí solo existían unas líneas, unos ángulos y unas cuantas operaciones aritméticas: trazos esenciales de una realidad astronómica.
Esa misma noche llamó a un trabajador de la biblioteca para encargarle una misión extraña: viajar en barco a Siena, esperar unos días, ver dentro del pozo y, ¡por Hermes!, recorrer a pie el largo camino de regreso, contando además cada uno de sus pasos.
Afortunadamente, él era el bibliotecario en jefe de la mejor biblioteca del mundo. Era el siglo II a.C. y el poderío de Alejandría sobrepasaba al de la propia Atenas. Habían pasado un poco más de cien años desde que Alejandro Magno conquistó Egipto y planeó su fundación. Él supo, en su gran imaginación también, que allí podía fundarse una ciudad espectacular. Con una mano en el Nilo y otra en el Mediterráneo: el centro de todo. Y así fue, aunque Alejandro no la viera jamás.
Pero sus generales, convertidos después en faraones, la tornaron capital del gran Egipto, centro de poder y de comercio en todo el mundo conocido. Alejandría llegaría a ser la segunda ciudad más grande e importante del mundo antiguo solo después de Roma. Y puesto que él, Eratóstenes, era el bibliotecario en jefe de la majestuosa biblioteca podía ordenar a un hombre que fuera a Siena, llegara hasta un determinado pozo y volviera caminando. El hombre midió, en efecto, su recorrido de regreso: 5000 estadios, según la medida antigua; 800 km actuales.
Eratóstenes arriba después al lugar del experimento: en una esquina de la plaza se hallaba el pozo. Clava ahí su bastón y espera un poco. Llegado el mediodía se asoma repetidas veces. Le complace lo que mira. Mide la longitud de la sombra del bastón. ¡Y eureka!, lo ha descubierto.
Un rato más tarde, con una sonrisa en el rostro, regresa a la biblioteca. Allí le basta con un dibujo. Un triángulo. Conocía dos de sus lados. La escala del esquema no importa porque el ángulo buscado es el mismo, siempre y cuando los lados del dibujo sean proporcionales al bastón y a la sombra: los triángulos proporcionales conservan los mismos ángulos.
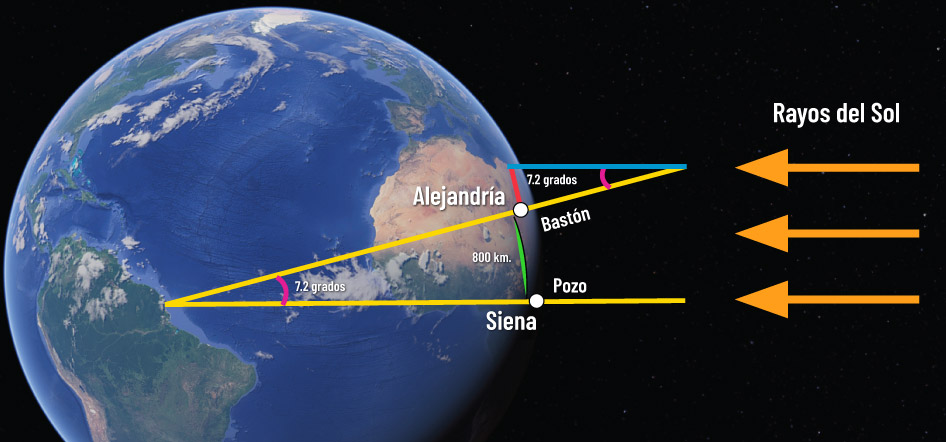
Siete grados. Siete grados era el ángulo de la sombra en Alejandría. Siete grados es el ángulo entre las líneas prolongadas imaginariamente del pozo de Siena y la del bastón de Eratóstenes, encontrándonos en el "centro de la Tierra".
Siete grados caben alrededor de 50 veces en la circunferencia. Siete grados corresponden a 800 km, según contabilizó caminando el cansado emisario. Y 50 veces 800 km son 40,000 km. Ese es el tamaño de la Tierra entera, su perímetro. Resultaba asombrosamente preciso. Sobre todo tomando en cuenta que para hacer su cálculo únicamente usó unos pies, un bastón, un pozo y el poder de la imaginación.
Le Verrier
Todo empezó con una hipótesis a la que llaman Ley. Aunque, más bien, todo empezó con un acto fortuito y un fantasma escapista. Realmente todo empezó con una mítica manzana y terminó con un falso planeta; ah, y un genio en un elevador.
Kepler descubre que las órbitas de los planetas son elípticas. Newton descubre las fórmulas para el cálculo de las órbitas planetarias. Hershell descubre por casualidad la existencia de Urano. Después de dar una primera vuelta al Sol desde que fue descubierto, Urano no está donde debería. ¿Qué puede provocar la pérdida de rumbo a todo un planeta?
Los planetas (del latín planeta “vagabundo", "errante”,) han jugado un papel importante en la cultura humana desde tiempos inmemoriales y han sido objeto de observaciones constantes. Su posición siempre fue móvil con respecto a las estrellas que, hallándose mucho más lejanas, hacen de fondo al recorrido de todos ellos alrededor del Sol. Al estar todos los planetas prácticamente en el mismo plano, vistos desde la Tierra, sus posiciones siempre están viajando a través de una franja o cinturón de constelaciones de fondo, a este plano se le ha llamado "eclíptica". Cada uno a su velocidad. Mientras más lejos, más lento viajan. Cuando completan un ciclo alrededor del sol, ha pasado lo que llamamos un año de ellos. Obviamente, el año Jupiteriano es mucho más largo que el de Venus o el de la Tierra: dura doce años terrestres. El de Marte 1.8, el de Venus 0.7.
Estudiando la trayectoria de Marte gracias al excelente observatorio de Tycho Brahe, Johannes Kepler descubrió, muy a su pesar, que la órbita de ese no era circular y "perfecta". En cambio, describía una elipse -de la cual, el círculo no es más que es un caso particular- cuando sus dos focos coinciden. Esto rompía con todo su modelo de sistema solar fuertemente basado en una representación divina de un orden superior. Sin embargo, una vez que la evidencia fue contundente no tuvo más que aceptarlo y eso revolucionó el marco conceptual usado posteriormente para expresar y prever la posición de cualquier planeta.
Cien años después, el superdotado Newton establecía las bases de la mecánica celeste. Fundamentos que operan con toda precisión y son las bases del cálculo actual de órbitas de planetas, cometas y satélites. Cualquier nave hecha por humanos es lanzada al espacio gracias a los cálculos de trayectoria del buen Isaac.
En 1766 se publicó la Ley de Titius Bode, y esta asociaba el orden de cada planeta en sucesión con la distancia al Sol. Es decir, la distancia al Sol de un planeta se obtiene en función del lugar sucesivo ocupado en el sistema solar. Mercurio es el primero, Venus el segundo, etc. Y aunque se llama "ley", se trata de una teoría que casualmente se cumple en el sistema solar sin mucha precisión. Sin embargo originó sorprendentes resultados al ser utilizada después y dio lugar a un gran descubrimiento.
Ochenta años después de Newton, en 1781, William Herschel descubría por casualidad un objeto que cambiaba de posición a diferencia del resto de las estrellas de fondo. Su color azulado lo delataba: era Urano. Bueno, él lo bautizó "Jorge" pero finalmente la tradición de seguir con el árbol genealógico de la mitología griega ganó: Júpiter hijo de Saturno, Saturno hijo de Urano (Ouranós: firmamento). Sucedió a unos cuantos años de la publicación de la Ley de Bode y parecía confirmarla categóricamente.
Después de varios años, numerosos equipos de astrónomos, en diferentes partes del mundo se dieron a la tarea de observar a Urano luego de dar su primera vuelta al Sol desde que fue descubierto. Pero detectaron algo muy extraño: poco a poco, la posición real del planeta difería de los cálculos hechos con las ecuaciones newtonianas. Estas habían sido notoriamente precisas con otros planetas. ¿Cuál era la causa de aquel desajuste en Urano?
Una de las teorías más comunes para explicar esta diferencia era la posible existencia de otro planeta alterando con su gravedad la posición de Urano. Los cálculos eran complicados y retadores. En París, el director del Observatorio, Francois Arago, le encomendó esa tarea a Urbain Le Verrier, quien tenía 35 años de edad y era egresado de la École polytechnique. Haciendo un montón de suposiciones bastante audaces y utilizando la supuesta Ley de Bode, Le Verrier asumió la existencia de otro planeta misterioso que producía ese complejo efecto en Urano. Calculó la posición en la cual debería estar el sospechoso. En 1846 Le Verrier le solicitó a un amigo alemán, Johann Gottfried Galle, echar un vistazo en esa zona donde sus cálculos predecían la posición del planeta escapista. Y ¡sorpresa!: allí estaba el prófugo, cuyo intenso color azul marino le valió un nombre inspirado en el mar: Neptuno. ¡Le Verrier con ningún instrumento más allá de su lápiz y el poder de la imaginación descubrió un planeta!

Epílogo.
Años más tarde, emocionado por su descubrimiento, Le Verrier trató de aplicar la misma lógica al comportamiento irregular de Mercurio cada vez que daba vuelta alrededor del Sol. Imaginó otro planeta escondido siempre detrás del Sol y hasta nombre le pusieron. La búsqueda de Vulcano no logró nunca fruto alguno. Y no se supo la verdad hasta que otro gran “imaginador” locuaz y bigotón descubrió que la gran masa del Sol distorsionaba el espacio tiempo y provocaba las fluctuaciones en la órbita del planeta más pequeño y cercano. Y todo gracias al poder de la imaginación.
Ficha de autor
Luis Leñero Elu
Estudió Matemáticas en la Facultad de Ciencias de la UNAM. Es compositor, maestro y fundador del Instituto del Juego. Se ha dedicado a la enseñanza y la comunicación educativa aplicando tecnologías y gamificación en diversos ámbitos.



