
Ciertas nociones pueden conceptualizarse según estilos que son dictatoriales o democráticos. Por ejemplo, la propiedad de circularidad de la curva denominada circunferencia puede concebirse según dos estilos que lo expresan de manera diferente, aunque geométricamente sean equivalentes: (a) dictatorialmente, toda distancia entre el centro y cualquier punto exterior que pertenezca a la circunferencia debe ser una constante y (b) democráticamente, todo punto en una circunferencia está a una distancia de un punto interior llamado centro que es la misma para todos.
Desde un punto de vista cognitivo, las conceptualizaciones dictatoriales son negativas, restrictivas, centrífugas, van del centro a la periferia: “tienen que obedecerme todos esos puntos que están ahí en el exterior formando una circunferencia”. Las conceptualizaciones democráticas son atractivas, liberadoras, centrípetas, van de la periferia al centro: “nosotros, que estamos relacionados de manera circular formando una curva cerrada, discutimos y decidimos lo que debe hacerse desde el centro”.
Por supuesto, en términos generales hay diferencias y hasta oposición entre estos dos estilos de conceptualización. La equivalencia en la circunferencia es mera coincidencia matemática, culpa de Pitágoras y del hecho de que, en coordenadas cartesianas, la ecuación de la circunferencia es de la forma x2 + y2 = R2. Veamos porqué.
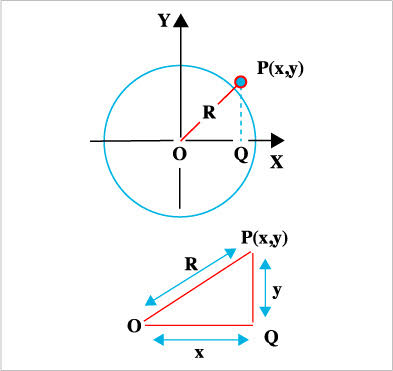
- Consideremos dos ejes mutuamente perpendiculares que se cruzan en el origen O: el eje horizontal de las abscisas X y el eje vertical de las ordenadas Y.
- Tracemos una circunferencia de radio R centrada en O.
- Seleccionemos un punto P de coordenadas x e y, que indicaremos como P(x,y), y bajemos una paralela al eje Y desde el punto P para intersectar al eje X en el punto Q.
- Recordemos que en el triángulo rectángulo OQP, los segmentos OQ y QP, así como OP, se denominan, respectivamente, catetos e hipotenusa.
- Apliquemos el teorema de Pitágoras al triángulo rectángulo OQP: (OQ)2 + (QP)2 = (OP)2.
- Consideremos que para todo punto P(x,y) de la circunferencia se forman triángulos rectángulos similares a OQP donde se cumple la relación pitagórica anterior, por lo que, identificando OQ con la coordenada x, QP con la coordenada y, y OP con el radio R, resulta x2 + y2 = R2.
La conceptualización de centralidad tuvo significativos avances en la Grecia antigua en cuestiones de política, arquitectura, geometría y astronomía. Tomamos como referencia la conferencia del antropólogo e historiador francés Jean-Pierre Vernant (1914-2007), Geometría y astronomía esférica en la primera cosmología griega, publicada en francés en 1963 en la Revista La Pensée. Durante la Segunda Guerra Mundial, Vernant encabezó en Toulouse la resistencia contra la ocupación alemana.
Con el fin de ubicarnos en la Grecia antigua, la siguiente Tabla indica lo más significativo de la época en tres aspectos: sucesos y obras escritas (primera columna), desarrollos en Matemáticas y Astronomía (segunda columna) y construcciones y contribuciones en ciencia y tecnología (tercera columna). Todas estas aportaciones se han clasificado en tres periodos, todos ellos anteriores a la era Cristiana, siguiendo el criterio de Will Durant.

Este artículo consta de dos secciones. En la primera sección consideramos la construcción de espacios circulares en la vida comunitaria y hacemos referencia al filósofo Ferécides de Siros (580 a.C. – 520 a.C.), al poeta Homero (siglo VIII a.C.) y al arquitecto Hipodamos de Mileto (498 a.C.- 408 a.C.). En la segunda sección abordamos el concepto de circularidad en relación con la definición de espacios geométricos y astronómicos; además, describimos aportaciones del poeta y filósofo Hesíodo de Ascra, Tebas (cerca de 800 a.C.) y del filósofo, geógrafo y físico Anaximandro de Mileto, Jonia (619 a.C. – 546 a.C.).
La construcción de espacios sociopolíticos y arquitectónicos
Antes de la aparición de las instituciones políticas en Grecia, en la organización social el rey-sacerdote ocupaba el nivel más alto; era un dictador que dominaba a la población en condiciones de sumisión. Los asuntos de interés público no se discutían; se ordenaban, imponían y acataban, siempre del centro a la periferia. No había oportunidades para comunicar ni para debatir.


En el canto II de la Odisea, Homero narra que Telémaco, el hijo de Ulises y Penélope, preocupado por alejar a los pretendientes que acosaban a su madre, convoca a un grupo de militares a reunirse en el ágora (del griego asamblea). Se atribuye a este mismo poeta la expresión ageirien laon, que quiere decir: juntar a la armada. Y es que los guerreros se agrupaban en formación militar haciendo una circunferencia y cuando alguien quería tomar la palabra pasaba al centro para expresarse muy democráticamente.
Fuente: https://www.biografiasyvidas.com/biografia/h/fotos/homero_2.jpg
Ante la comunidad, el ágora señalaba la aparición de instituciones en organizaciones centralizadas en lo político, con un centro en lo social, urbano y cultural. Era un espacio donde todos participaban; en el centro se aplicaba la ley en condiciones de igualdad, equilibrio, simetría y reciprocidad. Es notable observar la centralidad del ágora en el plano de la reconstrucción de la ciudad de Mileto (Figura 1), elaborado por el urbanista Hipodamos, alrededor del año 479 a.C.
Fuente: http://3.bp.blogspot.com/XLSEv87sndY/T4xNhiCULDI/AAAAAAAAAKQ/qdh4SkbUH-c/s200/grecia_arquitectohipodamosdeMileto.jpg

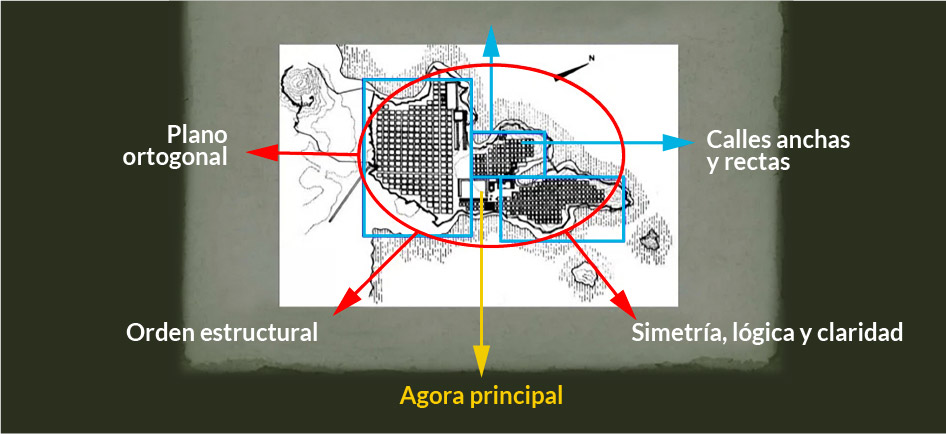
Figura 1. Plano de la reconstrucción de la ciudad de Mileto.
Fuente: https://image.slidesharecdn.com/hipodamodemileto-141007173559-conversion-gate02/95/hipodamo-de-mileto-5-638.jpg?cb=1412703392
La construcción de espacios astronómicos y geométricos
De acuerdo con Vernant, la nueva imagen de la sociedad democrática en Grecia es paralela a una nueva imagen del espacio astronómico y geométrico; conlleva cambios conceptuales donde las nociones de centro y centralidad son cruciales. Por el contrario, en momentos y lugares diferentes, el desarrollo de la astronomía babilónica sirvió de apoyo a una religión relacionada en el conocimiento de los astros, concebidos como divinidades cuyas intenciones podían percibirse si se observaban sus posiciones.
Quienes escudriñaban el cielo babilonio eran escribas al servicio del rey, con la obligación de registrar la actividad económica del reino y contabilizar los acontecimientos terrestres y celestes. Aportaron a la construcción del conocimiento siguiendo órdenes reales, pero tan solo realizaron cálculos aritméticos, para nada conectados a un sistema geométrico de representación espacial de posiciones y movimientos. Desarrollaron la noción de circularidad dictatorial.
Por su parte, la astronomía griega, desligada de toda religión, propuso explicaciones acerca de la estructura y el funcionamiento del mundo sin referirse a divinidades o a prácticas de rituales. Aunque estuvo llena de creencias míticas, aceptaba aportaciones diferentes, elaboradas con el fin de que los demás también entendieran cómo estaba el mundo. Se empezaba a desarrollar la noción de circularidad democrática.

Según Hesíodo, la Tierra era una vasija dentro de la cual se encontraba el mundo encerrado por Zeus para evitar que saliese a la luz el mundo subterráneo del desorden. Era un universo de espacios estructurados: en el nivel superior Zeus y los dioses inmortales, en el segundo los hombres y en el tercero la muerte y los dioses subterráneos. En este universo mitológico la Tierra permanecía estable en un espacio circular y debía apoyarse en algo que le daba sustento y respecto de lo cual dependía.
Fuente: http://k43.kn3.net/05F668AAE.jpg
Sin embargo, los físicos jónicos se opusieron a esa imagen enclaustrada de la sociedad y del universo. Pertenecieron a esta escuela de pensamiento: Tales (624 a.C. – 546 a.C.), su discípulo Anaximandro (610 a.C. – 546 a.C.) y Anaxímenes (590 a.C. – entre 528 y 525 a.C.); todos ellos nacidos en Mileto, Jonia. Para ellos, la mitología era dictatorial, limitada e insuficiente; buscaron explicaciones racionales propias de un replanteamiento democrático de la representación e interpretación del espacio en el universo.

En la Grecia antigua la noción de circularidad fue significativa; tuvo consecuencias en la construcción del espacio urbano y en la organización política donde el ágora fue el centro de las discusiones y las decisiones. Dicha noción coexistió de manera análoga con la conceptualización de un espacio geométrico para explicar la forma de la Tierra y de un espacio astronómico para dar una idea de la estructura del universo. Así nació la ciencia griega: primero el abandono de la dictadura del dogmatismo y la superstición; luego la democratización del acceso al conocimiento y la libertad para su comunicación, discusión, aplicación y transformación.
Referencias
Durant, W. (1966). The story of civilization. 2. The Life of Greece, New York, Simon and Schuster.
Hellemans, A. y Bunch, B. (1988). The Timetables of Science. A Chronology of the Most Important People and Events in the History of Science. New York. Simon and Schuster.
Vernant, J.P. (1963). Géométrie et astronomie sphérique dans la première cosmologie grecque. Revista La Pensée.
Ficha del autor
Jorge Barojas Weber: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Profesor del Departamento de Física de la Facultad de Ciencias y tutor en el Doctorado en Ciencias de la Administración (línea de investigación en administración del conocimiento), ambas de la UNAM. Ha sido investigador adscrito a la Unidad Académica del ILCE.



