
Dedico este artículo a mostrar cómo las matemáticas sirven para comprender lo que sucede en nuestro entorno y en el universo. Ilustraré dos casos relacionados con el tiro parabólico: la trayectoria que sigue una pelota en un juego de béisbol, desde que le pega el bateador hasta que la atrapa un jardinero, y los rebotes sucesivos de una pelota que cae. Ambos son ejemplos de como el cerebro aprende y usa las matemáticas.
Descripción de trayectorias parabólicas
¿Tienes idea de los cálculos que debe hacer un jardinero cuando escucha que el bateador ha conectado la pelota y debe decidir qué hacer para atrapar esa pelota antes de que toque el suelo? ¿Por qué después de lanzar hacia arriba una pelota, esta desciende, pega en el suelo y rebota a alturas cada vez menores?
Utilizando las matemáticas podemos comprender con facilidad estos curiosos fenómenos cuando entendemos cómo se mueven los cuerpos y qué produce los movimientos que observamos.
Comenzaré diciendo que todos los cuerpos que se mueven en nuestro planeta (piedras, flechas, jabalinas, balas, pelotas, automóviles, aviones, …) describen trayectorias en términos de líneas rectas, arcos de circunferencias, parábolas y otras curvas más complicadas.
Las fuerzas mecánicas, como empujones y jalones, son las causantes del cambio en el estado de movimiento de los cuerpos: si están parados empiezan a moverse o si están moviéndose cambian su velocidad cuando se frenan o aceleran. Además, si los cuerpos están cerca de la superficie de la Tierra, experimentan las consecuencias de la fuerza de atracción gravitacional, la cual provoca que baje toda masa que sube.
Consideremos una pelota que describe una trayectoria parabólica como consecuencia de un batazo. El movimiento de la pelota está determinado por dos fuerzas: la que aplica el bateador a la pelota para que esta adquiera cierta velocidad inicial y la fuerza de gravedad que frena el movimiento ascensional de la pelota, la detiene por un instante cuando alcanza la altura máxima y luego la acelera hacia abajo obligándola a descender.
Esta trayectoria se caracteriza por dos parámetros: la altura máxima h a la cual sube la pelota y el alcance R que corresponde a la distancia que va desde el punto del que sale la pelota hasta el punto al que llega al suelo (Figura 1). En dicha figura se indica que la pelota empieza a moverse en el punto O, la velocidad inicial se representa por el vector v0 (flecha en rojo) y la fuerza de gravedada por el vector Fg (flecha en azul).
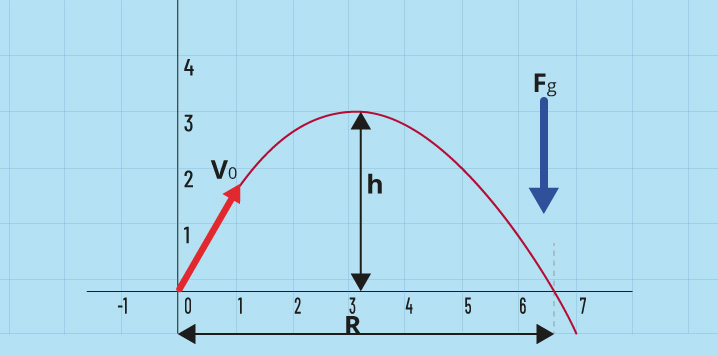
Figura 1. Trayectoria parabólica de una pelota y parámetros característicos
¿Cómo se produce el movimiento parabólico? En el Anexo 1 muestro cómo la trayectoria de una parábola se debe a la composición de dos movimientos: uno en sentido horizontal con velocidad constante y otro en la dirección vertical que comienza con un valor inicial de la componente de la velocidad en esta dirección. Esta velocidad va disminuyendo por efecto de la aceleración negativa de la fuerza de gravedad, llega a un punto donde se anula y luego se incrementa hasta alcanzar el mismo valor que tenía al principio pero en una dirección contraria.
Batear y atrapar pelotas en el béisbol
Pensemos ahora en un juego del béisbol y, muy concretamente, en el momento en que un bateador le pega a la pelota, esta describe una parábola y finalmente es atrapada por uno de los jardineros, tal como se muestra en la siguiente secuencia.

Si un pitcher lanza a 95 millas por hora (42.45 metros por segundo), la pelota tarda 0.42 segundos en recorrer la distancia de 60 pies y 6 pulgadas (18.15 metros) que existe entre la posición del pitcher y el lugar donde está colocado el plato en el home. Esto significa que el bateador tiene menos de medio segundo para estimar por dónde pasará la pelota y mover su cuerpo para conectar el batazo (Figura 2a).
Figura 2a. Primera etapa para atrapar un batazo: el bateador le pega a la pelota.
Si despreciamos la fricción con el aire y no hay viento, la pelota describirá una parábola en un plano. En esas condiciones la pelota viajará una distancia correspondiente al alcance de la parábola R, que supondremos es de 100 m. Además, consideraremos que la parábola caerá entre los jardineros J1 y J2, muy cerca de la barda del parque, que está a 350 pies (107 m) del home. (Figura 2b).
Figura 2b. Segunda etapa para atrapar un batazo: la pelota describe una parábola.
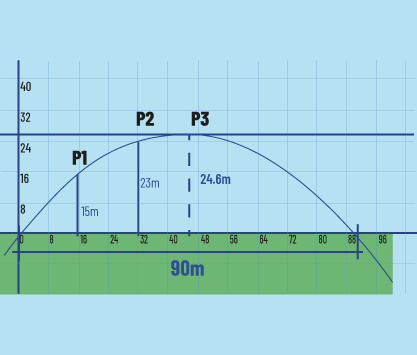
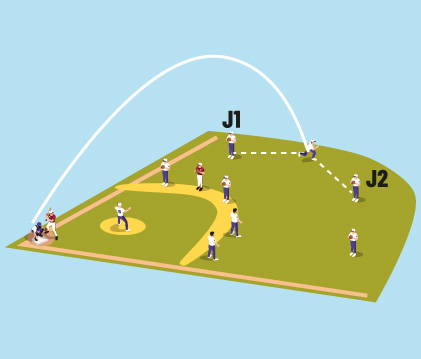
Figura 2c. Tercera etapa para atrapar un batazo: los dos jardineros J1 y J2 observan cuando la pelota pasa por las posiciones P1, P2 y P3 y deciden quién ha de correr para atraparla.

Usualmente, el jardinero que está más cerca del lugar donde caerá la pelota es el primero en correr. Ya habrá considerado previamente los tiempos, las distancias y las velocidades de dos trayectorias: la de la pelota que describe la parábola y la suya propia, concretamente la del guante con el que atrapará la pelota. Durante muchos entrenamientos habrá practicado para que la pelota y su guante coincidan en el mismo lugar, al mismo tiempo. (Figura 2d).
Figura 2d. Cuarta etapa para atrapar un batazo: atrapadón del jardinero izquierdo J1.
Los rebotes sucesivos de una pelota
¿Cómo se obtiene la curva que representa los botes sucesivos de una pelota que después de cada impacto con el suelo sube a una altura menor?
La Figura 3 nos muestra tres curvas: en rojo aparece una sucesión periódica de arcos de parábolas que se repiten, siempre alcanzando la misma altura; en verde una recta inclinada cuya altura va decreciendo y en azul lo que corresponde al bote amortiguado de la pelota.
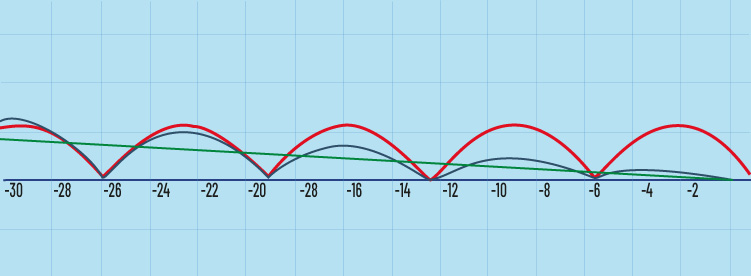
Figura 3. Aspectos de la trayectoria de una pelota que rebota.
Procederé en etapas y empezaré por la parábola simple, que describe una pelota que parte del origen, sube, llega a su máxima altura y luego decae hasta llegar al suelo. Para lograr que esta parábola se repita utilizaré una función periódica senoidal del tipo, caracterizada por dos parámetros: A (su amplitud) y B (su fase). Ajustaré estos parámetros para que el primer ciclo de la función periódica (curva en verde) se parezca mucho a la trayectoria de la parábola (curva en rojo), tal como se observa en la figura 4a.
Esta función senoidal tiene dos características importantes: (1) como durante el primer ciclo de la función senoidal son muy pequeñas las diferencias con los valores de la curva parabólica, las superficies bajo cada curva son prácticamente iguales y (2) la periodicidad de la función senoidal nos permite lograr una repetición similar a la de los botes de la pelota, cuando se considera únicamente el valor absoluto de la función senoidal.
El valor absoluto de la función senoidal completa se indica como y=A‖sen(Bx)‖, lo cual sigifica que se mantienen los ciclos con valores positivos (ordenadas arriba del eje de las abscisas) mientras que se invierten los ciclos con valores negativos (ordenadas abajo del eje de las abscisas), tal como lo indica la figura 4b.
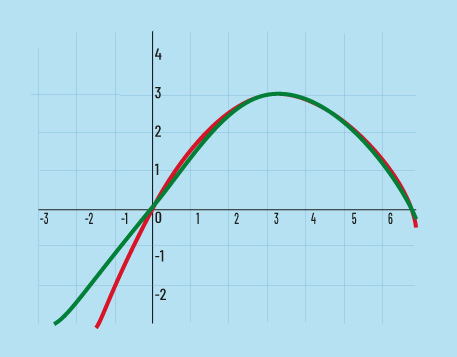
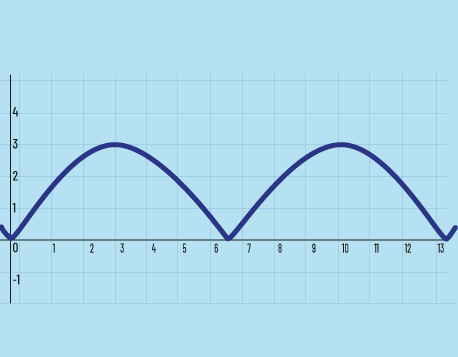
Figuras 4a y 4b. Comparación de una parábola con el primer ciclo de una función senoidal (a) y representación del valor absoluto de una función senoidal (b).
Sin embargo, las alturas a las cuales rebota una pelota disminuyen gradualmente porque los choques de la pelota con el suelo no son perfectamente elásticos. Esto significa que la velocidad con la cual sale la pelota que rebota es menor a la velocidad con la cual llega al suelo. Lo anterior implica que la amplitud A del valor absoluto de la función senoidal no es una constante sino una función del tipo que corresponde a una recta de pendiente m negativa, como la indicada en color verde en la figura 3. En otras palabras, la curva que representa los botes sucesivos de la pelota corresponde a la ecuación.
Conclusiones
Los dos casos considerados en este artículo ejemplifican cómo es que las matemáticas nos ayudan a comprender fenómenos. En esta tarea es esencial poder hablar el lenguaje de las matemáticas sin entrar en detalles formales ni tener que perderse en la selva de las abstracciones.
Lo significativo es que el cerebro humano tiene la capacidad de hablar el lenguaje de las matemáticas. Se ha ido entrenando a medida que evoluciona el ser humano y la educación, no memorística, reactiva sus estrategias de solución de problemas y propicia exitosas experiencias de aprendizaje.
El cerebro de los seres humanos tiene una gran capacidad para entender cómo es que una pelota robota y su altura disminuye, una vez que se le explica, de manera clara, sencilla y directa, cómo interpretar la trayectoria complicada en términos de funciones elementales que se superponen y modifican. En este caso no es necesario hacer los cálculos; basta pensar para comprender las imágenes.
Es sorprendente la capacidad de los jardineros que atrapan pelotas en el bésibol porque han aprendido a estimar trayectorias en tiempos sumamente cortos. No han recibido clases de matemáticas acerca de cuál es la trayectoria de una parábola ni cómo calcularla. Esta capacidad se ha desarrollado después de un gran número de entrenamientos y la puesta en práctica en muchos juegos durante la temporada. Saben y aplican matemáticas sin saberlo.
¿A qué se debe entonces que la mayor parte de los estudiantes piensen que las matemáticas son muy difíciles y, además, de muy escasa utilidad? Espero que la lectura de este artículo les permita comprender dos cosas:
- Que todos los seres humanos contamos con la capacidad para realizar estimaciones y hasta cálculos matemáticos en nuestra vida cotidiana y que ello no es una habilidad que puedan desarrollar solo unos cuantos.
- Que las matemáticas son extraordinariamente útiles para resolver problemas muy diversos, incluyendo los deportes y la mayor parte de las acciones que realizamos en nuestra vida cotidiana.
ANEXO 1. Obtención de la ecuación de la parábola

Ficha del autor
Enrique Calderón Alzati (q. e. p. d.):
Doctor en Ciencias de la Computación y la información por la Universidad de Pennsylvania. Autor de varios libros, articulista de La Jornada. Director General del Instituto Latinoamericano de la Comunicación Educativa (ILCE).



