

Figura 1. Douglas R. Hofstadter
El autor
Douglas R. Hofstadter, Doctor en Física, Graduado en Matemáticas, hijo de un Premio Nobel y ganador del Pulitzer tuvo a bien lanzar al mundo este libro en 1979. En él encuentra una intersección, y muestra una raíz común, entre tres espacios de la exploración humana: la plástica, la música y las matemáticas. En estos campos, algunas mentes brillantes han descubierto las peculiaridades de los procesos autorreferenciales, del mirar sobre sí mismo, donde la obra conecta forma y significado. Este puente, fuente de conciencia, vuelca la obra sobre sí misma, y en ese auto-conectarse surgen sorprendentes paradojas. Detrás de cada una, hay una puerta secreta que se abre a la multidimensionalidad, al sentido revelado de la forma, la aparición del símbolo, la metáfora, la paradoja, y finalmente la analogía, como bloque primordial del conocimiento.
La autorreferencialidad es una noción intrínseca a las revelaciones más antiguas y profundas de la creación y el origen de la existencia: El Ouroboros, dragón que se devora la cola, representa el giro del movimiento cósmico. Significa que la creación divina requiere el sacrificio del Dios, como sucede en la tradición Teotihuacana: la ceremonia del nuevo Sol. También en la cosmogonía de los Vedas aparecen las dos aves primordiales, una comiendo y otra mirándola comer: Arjuna y Krishna.
El libro
Gödel, Escher, Bach: Una eterna trenza dorada es un gran libro que rebasa, por mucho, el nivel divulgativo y explica cómo, en diferentes disciplinas, un mismo concepto se manifiesta conectando actos de exploración profunda por parte de mentes geniales. Bach en la música, Escher en el dibujo y Gödel en las matemáticas. Este libro explora lo que revela esa trenza, ese bucle, el poder de voltear sobre sí mismo. Y aborda diversos temas a través de diálogos y reflexiones, donde la forma del escrito manifiesta a su vez el contenido del texto. Es decir, se “auto-refiere”. Tal autorreferencialidad es el sello común. La obra es consciente de sí misma.

Figura 2. Gödel, Escher, Bach: Una eterna trenza dorada

Figura 3. Autorreferencialidad
Autorreferencialidad y Paradojas
“Esta frase tiene cinco palabras”. La frase anterior es inocentemente peligrosa. Es el lenguaje hablando sobre sí mismo. Palabras sobre las palabras. Hay dos niveles, el nivel del lenguaje y el nivel de la reflexión sobre el lenguaje. La veracidad o significado de la frase se remite a sí misma, en particular a su dimensión o tamaño. Sin embargo podemos construir frases que sean autorreferentes de manera provocadora: “Esta frase es una mentira”. Si la frase es verdadera entonces tendremos que aceptar que lo que dice es verdad. Pero ¿qué dice? Dice que es mentira. Caemos en una paradoja autorreferente. El dragón mordiéndose la cola.
Recursividad
Una manera de referirnos a esta autorreferencialidad es a través del concepto de Recursividad. En matemáticas la recursividad frecuentemente permite definiciones de conjuntos o series, por ejemplo, la definición de los números naturales:
n es un número Natural si:
- n=1 ó
- Si existe un número m que sea Natural y n=m+1
Es decir que la definición de ser n un natural depende de que el número que le preceda sea Natural.
También la Recursividad aparece frecuentemente en la conformación de series de números. Como ésta definición de los números pares, por ejemplo:
Pn = P (n-1) + 2
Que no dice otra cosa que “un número par se obtiene sumando 2 al par anterior”.
Otra asombrosa manifestación de recursividad se ve en la generación de objetos matemáticos de dimensión fractal. Ejemplo de eso el conjunto de Mandelbrot.

Figura 4. Fractal
Fondo y forma
Esta eterna trenza dorada, GEB, tiene mucho de juego de formas, de bucles y giros, tanto del texto como de las ideas. Expresa, justamente de manera recursiva, cómo la recursividad aparece en la trascendente obra de Johan Sebastian Bach, en la obra genial de M.C. Escher, y en la creación conmocionante del matemático Kurt Gödel. Es símbolo de la misma conciencia humana y revela una profundidad filosófica sobre la realidad del mundo y el conocimiento.
La analogía
En el fondo, la analogía es una forma cognitiva. Un buen ejemplo: el principio de dualidad. En la geometría sucede algo sorprendente. Conocemos los principios básicos sobre puntos y líneas. Y sabemos que hay una íntima relación entre ambos, los unos producen los otros y viceversa. Dos líneas definen un punto y dos puntos definen una línea. Sin embargo aquí surge un descubrimiento inesperado: Cualquier afirmación verdadera que incluya las palabras “punto” y “línea” al invertir dichos términos genera una afirmación también verdadera. Una analogía proyecta todo un campo de significación en otro campo, en otro ámbito. Proyecciones o transformaciones les llaman los matemáticos. La vinculación de elementos a otros por medio de la relación por analogía revela una relación secreta de alguna manera invisible, que permite usar lo que se ha pensado en un campo de estudio para revelar relaciones y propiedades en otro campo diferente. En particular la reflexión sobre correspondencia de aseveraciones matemáticas (teoremas) entre sí, está pero en otro nivel: la Metamatemática.
¿Cómo la recursividad se manifiesta en la obra de Escher?

Figura 5. Fondo y figura
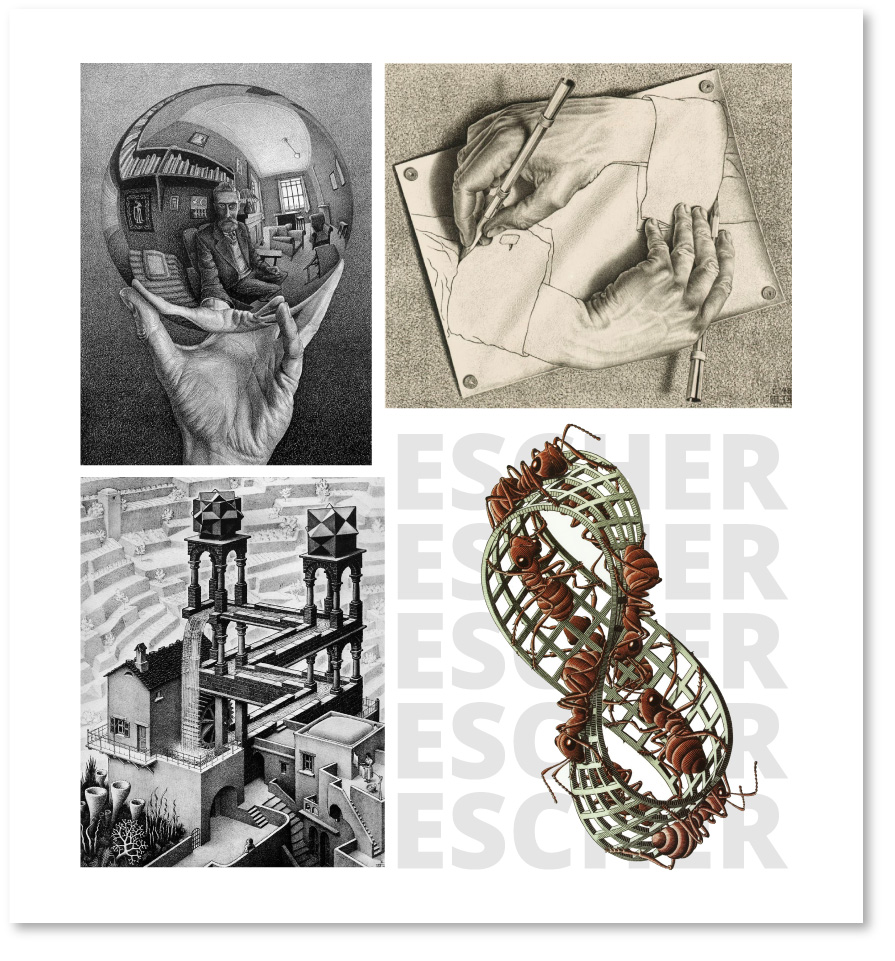
Cómo la recursividad se manifiesta en la obra de Bach?
Bach, "Little" Fugue in G Minor BWV 578 "free mp3"
JS Bach BWV 1079 Canon Cangrejo en Banda Moëbius
Y ¿Cómo la recursividad se manifiesta en la obra de Gödel?
Los sistemas formales
Gran parte del conocimiento científico se basa en una estructura de pensamiento y un universo de objetos definibles. Los objetos y las relaciones en el sistema formal o modelo buscan, en términos generales, una correspondencia a objetos y relaciones de un ámbito concreto o particular ya sea una galaxia, un ecosistema, una población, o la corteza terrestre.
Los principios fundamentales en nuestro sistemas formales son las reglas del juego, llamados Axiomas. A cada jugada posible aplicando los Axiomas se le llama Teorema.
Y ya que nuestro universo de objetos abstractos se corresponden con los objetos del campo a modelar, podemos explorar las relaciones y sus propiedades mediante la manipulación de las representaciones correspondientes en el sistema formal. El uso de modelos es la forma canónica de hacer ciencia. En los modelos podemos predecir y entender los sucesos del mundo representado.
En particular se han creado muchos modelos axiomáticos que buscan ser completos para representar diferentes áreas de estudio dentro del universo matemático. La teoría de conjuntos logró definir un sistema axiomático muy poderoso y fundamental llamado Sistema Axiomático Zermelo Fraenkel para la Teoría de Conjuntos.
La lógica se encargaría de construirlo todo y todo lo construido sería verdadero. Todo lo enunciable sería comprobable. El sistema sería completo al fin. Y por un tiempo al menos ese paraíso pareció haber llegado para quedarse. Pero más pronto que tarde, llegó un amigo de Einstein a romper esa ilusión.

Figura 7. Kurt Gödel con su amigo Albert Einstein
El Teorema de Incompletud de Gödel
El universo donde se llegó a este teorema es el de la teoría de axiomas de la Aritmética. El sistema axiomático de la Teoría de Conjuntos de Zermelo Fraenkel parecía tener las dos virtudes mágicas. La primera es la propiedad de ser consistente. Es decir que no puedes demostrar que algo sea verdadero y demostrar que eso mismo es falso a partir de los mismos axiomas. La segunda es la completud, es decir, que de cualquier cosa que pueda ser enunciada puede demostrarse su veracidad o falsedad. Es decir que el modelo abarca todos los objetos de un universo.
Gödel en su impresionante demostración, usa esa propiedad intrínseca a los lenguajes naturales, la capacidad de mirarse a sí mismo, la recursividad y la autorreferencialidad. Gödel descubre una frase que puede ser pronunciada pero que no puede ser demostrada. Descubre que si el sistema es consistente nunca podrá ser completo. Adiós al sueño. Que por más bueno que sea el sistema siendo consistente siempre habrá proposiciones indemostrables.
¿Qué significa todo esto?
Que los planteamientos autorreferenciales logran conectar niveles diferentes de significación, que son cuña y grieta para los sistemas formales. Que detrás de varias disciplinas ese mismo recurso revela fronteras, zonas indeterminadas donde habitan descubrimientos inesperados. Sin embargo, incluso del otro lado de la indeterminación cabe la reflexión sobre la veracidad objetiva (no tanto demostrable) de las cosas y sobre una realidad platoniana de aquellas proposiciones indemostrables ahora ya independientes, que pueden dar luz sobre otras cosas y ser fructíferas o no. Esto ha marcado un nuevo criterio para la exploración de esos “Caballos de Troya” que vencieron al sistema. Una de estas proposiciones independientes es la famosa hipótesis del continuo de Cantor de la cual ya hablamos en el artículo de los números transfinitos. ¿Existe algún infinito mayor que el de los números Naturales pero menor que el de los números Reales? Pregunta que se escapará elusivamente de cualquier demostración dentro del sistema axiomático de las matemáticas.
REFERENCIAS
Hofstadter, D. (1982). Godel, Escher, Bach Una eterna trenza dorada. México: CONACYT.
Ficha del autor
Luis Leñero Elu: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Estudió Matemáticas en la Facultad de Ciencias de la UNAM. Es compositor, maestro y fundador del Instituto del Juego. Se ha dedicado a la enseñanza y la comunicación educativa aplicando tecnologías y gamificación en diversos ámbitos.



