
Figura 1. Georg Cantor
En la segunda mitad del siglo XIX se desarrolló por primera vez una teoría formal sobre el infinito y los conjuntos. Extrañamente, a diferencia de muchos otros grandes avances en las matemáticas y las ciencias, esta fue creada prácticamente por solo un hombre: Georg Cantor. Nacido en San Petersburgo se mudó muy joven a Alemania que en aquella época era la sede más pujante e intensa de las matemáticas mundiales. Ahí nacieron la Teoría de Conjuntos y la Teoría de los números transfinitos.
Su trabajo fue recibido con escepticismo por parte de algunos, pues en particular, su teoría de los números transfinitos trastocaba nociones aceptadas desde la antigüedad en muchos diversos campos del pensamiento humano: la filosofía, la religión, las matemáticas, la lógica y las ciencias. ¿Cómo representar matemáticamente a los conjuntos y sus “tamaños” o cardinalidad? ¿Qué marco fundamental se necesitaba para poder definir y manipular dichos “números”? ¿Qué tipo de aritmética se podría desarrollar con estos números transfinitos? Al responder estas preguntas Cantor estableció las reglas para que la matemática pudiera investigar y comprender uno de los conceptos más vagos y complejos: el infinito.
Los Conjuntos y su tamaño
Cada vez que podemos definir una característica en común de varios elementos estamos, sin ir más lejos, declarando la existencia de un conjunto. Por ejemplo, si mencionamos la característica de los seres humanos de ser zurdos esto implica inmediatamente formar un conjunto de todos los humanos zurdos.
Al número de elementos que forman un conjunto se le llama cardinalidad. Por ejemplo, la cardinalidad del conjunto de los dedos de tus manos es 10. Y una manera de comparar dos conjuntos es creando parejas entre los elementos de uno y del otro. Si cada elemento de uno de los dos conjuntos tiene una y solo una pareja del otro conjunto podemos decir que los dos conjuntos tienen la misma cantidad de elementos o la misma cardinalidad.
Si tomamos el conjunto de los números del 1 al 10 y contamos los dedos de las manos, emparejamos uno a uno cada dedo con un número. Y podemos concluir que la cardinalidad de los dedos de las manos es 10 y la cardinalidad de los números del 1 al 10 es 10 también. Es decir, tienen la misma cardinalidad. Realmente, el hecho de emparejar un conjunto a algunos de los números naturales es lo que llamamos CONTAR.
Los números hacen conjuntos
Hablemos de números. Los números con los que contamos son los más intuitivos y naturales a los que estamos expuestos desde nuestra primera infancia. Y a todos ellos se les llama justo así: Naturales. ¡Y a decir verdad, se trata de un conjunto muy grande!
Y ¿cuál es su cardinalidad?; o sea ¿cuántos números naturales hay? Ah caray…
Pues sabemos que no tienen límite, es decir que no hay un número más grande que todos. Porque si decimos que G es un número natural más grande que cualquier otro, estaríamos mintiendo, dado que G+1 es también un número natural, y es más grande. Aquí es donde aparece la idea de Infinito.
La noción de infinito, pese a ser compleja, es un concepto muy usual y se emplea en muchos ámbitos de la vida y del conocimiento. Aunque al parecer contradiga nuestra percepción inmediata, finalmente resulta fácil entenderla a partir de la noción de lo ilimitado.
Comparar emparejando
Concentrándonos en el campo de las matemáticas, vemos que cuando aparece la noción de infinito empiezan a suceder cosas raras, anti-intuitivas.
Imaginemos el conjunto de todos los números Naturales. Es infinito. Ahora imaginemos el conjunto de los números pares. Pues aunque supuestamente serían la mitad de los números Naturales, son también infinitos. Y además si emparejamos ambos conjuntos, resulta que sí podríamos relacionar cada uno de los números pares con un número natural, sin detenernos. Esto implica, pues, que ambos conjuntos tienen la misma cardinalidad, ¡que son igual de grandes!
Cada cual tiene una sola pareja. Sabemos que a cualquier número Natural, llamémosle m, lo podemos emparejar con 2m, y simultáneamente sabemos que un número par cualquiera, llamémosle p, es el doble de “algo”, ese algo es un número natural que se llamaría s; así que podemos decir con toda seguridad que... p = 2 x s; esto significa que, a todo número p le podemos asociar un número natural s (que viene siendo el doble suyo: 2m) ¡Ah carambas!
Esto tiene una consecuencia asombrosa y extraña: Hay la misma cantidad de números Naturales que de números pares. Son conjuntos igual de infinitos.
Otros números, otros conjuntos ¿más grandes?
¿Y los Naturales son todos los números que conocemos? ¿Qué hay de los números negativos? El -1, el -2, el -3, etc. Pues bien, si al conjunto de los números positivos (los Naturales) le agregamos los mismos pero con signo negativo, se forma un nuevo conjunto que los matemáticos llaman el conjunto de los Enteros , a los que se representa con la letra Z. Acá nos va a suceder lo mismo que con los naturales y los pares. Si encontramos un emparejamiento de uno a uno entre los Naturales (N) y los Enteros (Z) sabremos que ambos conjuntos tienen la misma cardinalidad, es decir, son igual de grandes. Mira cómo se pueden relacionar los elementos de cada conjunto:

Así pues, si cualquier número entero z es positivo lo asigno a (2z) - 1 (es decir: lo multiplico por 2 y le resto 1); y si z es negativo lo asocio a (es decir: lo multiplico por -2).
Por lo tanto, los Enteros (Z) y los Naturales (N) tienen la misma cardinalidad, es decir son igualmente infinitos. ¿Cómo que “igualmente”? ¿Acaso puede haber infinitos “no iguales”? ¡¿Hay infinitos mayores a otros infinitos?!
Los Racionales
Hasta ahora todos los infinitos que les he presentado son igual de grandes. Vamos con el conjunto que les sigue. Es el conjunto de los llamados números Racionales, representados por la letra Q y son todos los números que se pueden expresar como una fracción o razón: siendo a y b números enteros. Todos los Enteros se pueden expresar como una fracción; por ejemplo 5 es equivalente a , y -8 que es equivalente a . Pero hay también muchos números que no son enteros pero que sí son fracciones; por ejemplo o . Otra vez nos encontramos con un conjunto que contiene a los anteriores y que parece infinito también. ¿Podremos emparejarlos?

Figura. 2. Modo de emparejamiento para la demostración de Cantor de que los Racionales son numerables.

Así, mientras podamos inventar un modo de enlistar un conjunto, aunque sea infinito será del mismo tamaño que los Naturales.
Por lo tanto, ya encontramos que N, Z y Q son infinitos de igual tamaño. Y que, extrañamente, los Naturales están contenidos en los Enteros y estos a su vez están contenidos en los Racionales.
En particular los Racionales tienen una propiedad que no tienen los Naturales o los Enteros. Siempre sucede que entre cualesquiera dos Racionales hay otro Racional. Esto no se cumple en los Naturales; por ejemplo: entre el 2 y el 3 no existe otro número Natural. En cambio si consideramos dos números Racionales p y q, resulta que es Racional y está justo en medio de p y q.
Un conjunto realmente más grande
Y... ¿ya se me acabaron los números? ¿Hay más?
Sí. Hay números que no son racionales y algunos de ellos son hasta famosos. Uno de los primeros que descubrieron los griegos fue la diagonal de un triángulo cuyos lados miden 1. y cuyo valor, según el teorema de Pitágoras es Raíz de 2.
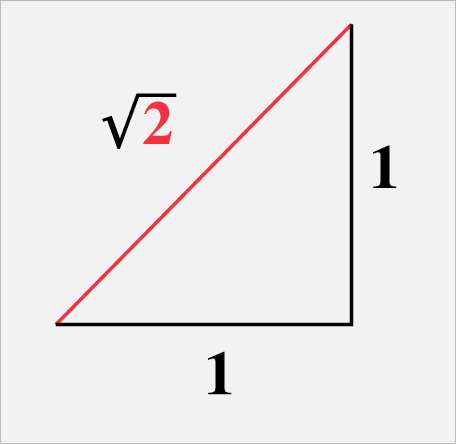
Figura. 3. El planteamiento de raíz de dos a partir del Teorema de Pitágoras.
Este número causó varias conmociones e incluso la muerte. En la secta de los Pitagóricos su existencia era casi una representación de algo extraño y maligno.
Otro número no racional es Pi Es decir, las veces que cabe el diámetro de un círculo en su circunferencia. Pi empieza así: 3.14159…….. y luego siguen una infinidad de números decimales, y por cierto sin ningún orden descubierto hasta la fecha.
Como estos números no son Racionales les llamaron Irracionales. Y al conjunto de los números Racionales unido al de los Irracionales se le llama conjunto de los números Reales. El panorama general queda así.
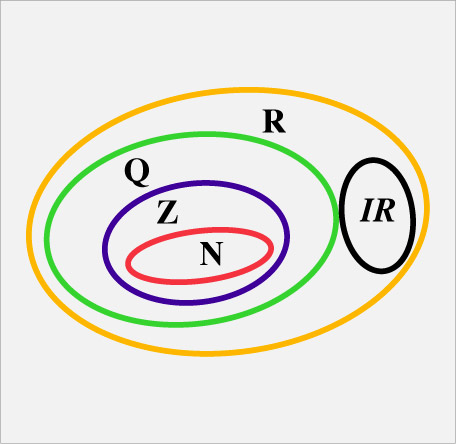
Figura. 4. Esquema de la contención de los subconjuntos de los números Reales.
Y aquí es donde se pone buena la cosa. Vamos a tratar de ver si el infinito de los Naturales, los Enteros y los Racionales es igual al de los Reales.
Vamos a tomar solo un subconjunto o parte de los Reales: todos los números que hay entre el Cero y el Uno. Y consideremos también al conjunto de los números Naturales.
Si pudiéramos encontrar un emparejamiento entre ambos conjunto, significaría que son igualmente infinitos. Es decir que los números Reales tienen la misma cardinalidad que los Naturales o como algunos dicen, que los Reales son numerables.
A veces los matemáticos cuando quieren demostrar algo que sospechan no es posible, justamente suponen que sí lo es y encuentran una contradicción. Usaremos esta técnica llamada reducción al absurdo.
Supongamos que podemos hacer un emparejamiento o lista numerada de todos los números contenidos entre el 0 y el 1. Supongamos que esa lista existe y que es completa. Es decir que todos los Reales entre 0 y 1 están en ella.
Esa lista sería así:
Recuerden que supusimos que dicha lista está completa; es decir, que todos los Reales entre 0 y 1 están en ella.
Fabriquemos un número:
Empezará con 0.
Y en el primer decimal ponemos un dígito diferente al primer decimal del primer número de la lista. Como el primer decimal del primer número de la lista es 0, pondremos un número cualquiera diferente a 0, por ejemplo: 2.
Ok. Entonces el número que estamos construyendo ahora es 0.2
Sigamos. Ahora pongamos como segundo decimal un dígito diferente al segundo decimal del segundo número de la lista, que es 3. Entonces elegimos un número diferente a 3, que sea 6.
Ahora nuestro número es 0.26 y así haremos sucesivamente para cada dígito, haciéndolo diferente del dígito correspondiente de cada número de la lista. Este número que acabamos de fabricar es diferente al primero de la lista porque difiere en su primer dígito. Es diferente al segundo de la lista porque difiere en su segundo dígito y así sucesivamente: nuestro número es diferente a cada uno de todos los de la lista. y además nuestro número es 0.26….. que es un número entre 0 y 1. Por lo tanto la lista no estaba completa.
Y así, siempre que pensemos que ya se pudo hacer una lista completa, podemos demostrar que le falta al menos el número que construimos. Y esto demuestra que no se puede hacer una relación de uno a uno entre los Naturales y los números Reales entre 0 y 1, y por supuesto mucho menos entre los Naturales y todos los Reales.
Por lo tanto, los números reales son infinitos pero un infinito más grande que el de los Naturales, Enteros o Racionales.
Todas las reuniones posibles de los miembros de un club
Si tenemos un club de juegos en el que se organizan reuniones semanales, y los miembros del club pueden asistir o no, veremos que las reuniones pueden contar con los siguientes asistentes:
Si los miembros del club son solo 2, digamos Arturo y Berenice, la reunión próxima puede ser de 4 maneras:
- Que lleguen todos, es decir Arturo y Berenice.
- Que solo llegue Arturo
- Que solo llegue Berenice
- Que no llegue nadie.
Tres de estos casos suenan muy aburridos, pero es que son solo 2 miembros y solo se dan 4 posibilidades.
Si entrara Carla al club, aumentan las posibilidades:
(Nota: se sombrean las posibilidades ya incluidas en el conjunto anterior).
| 1. Que lleguen todos |
| 2. Que lleguen solo Arturo y Berenice |
| 3. Que lleguen Arturo y Carla |
| 4. Que lleguen Berenice y Carla |
| 5. Que llegue solo Arturo |
| 6. Que llegue solo Berenice |
| 7. Que llegue solo Carla |
| 8. Que no llegue Nadie |
Bastó un nuevo miembro al club para que con 3 se llegara a 8 posibilidades.
Si entrara David al club tendremos más posibilidades:
| 1. Que lleguen todos |
| 2. Que lleguen solo Arturo, Berenice y Carla |
| 3. Que lleguen Arturo, Berenice y David |
| 4. Que lleguen Arturo, Carla y David |
| 5. Que lleguen Berenice, Carla y David |
| 6. Que lleguen solo Arturo y Berenice |
| 7. Que lleguen solo Arturo y Carla |
| 8. Que lleguen solo Arturo y David |
| 9. Que lleguen Berenice y Carla |
| 10. Que lleguen Berenice y David |
| 11. Que lleguen Carla y David |
| 12. Que llegue solo Arturo |
| 13. Que llegue solo Berenice |
| 14. Que llegue solo Carla |
| 15. Que llegue solo David |
| 16. Que no llegue nadie |
Esto quiere decir que si en el club hay 4 miembros, las posibilidades de reunión son 16. Resalté las posibilidades que estaban incluidas en los casos anteriores. Es decir, mientras aumentan los elementos, los subconjuntos previos quedan incluidos.
Retomando: Con un club de 2 miembros hay 4 reuniones, con uno de 3 hay 8, y con uno de 4 hay 16.
1-2
2-4
3-8
4-16
Estas parejas de números se pueden relacionar mediante una operación básica. Elevamos el número 2 al tamaño del club y nos da el número de reuniones posibles.
2 elevado a la 1 es 2 (=2)
2 elevado a 2 es 4 ( =4)
2 elevado a 3 es 8 =8)
2 elevado a 4 es 16. (=16)
Así pues, si queremos saber cuántas reuniones posibles hay en un club con 5 miembros, basta efectuar la operación =32.
Eso traducido a la jerga matemática se diría así:
Dado un conjunto de nombre N, con una cardinalidad n (número de elementos), el conjunto de todos sus subconjuntos tiene cardinalidad de 2 a la n.
Además, remarqué los casos del anterior club que quedan contenidos en el club de un miembro más.
Después de la tempestad viene...
Por último, podemos expresar cualquier número Real como un subconjunto de combinaciones de los números Naturales. Y esto tiene una consecuencia sorprendente.
Los números Naturales tienen cardinalidad infinita, llamémosle 0. La cardinalidad del conjunto de todos los subconjuntos de los Naturales, es decir de los Reales será 2 elevado a la 0. es decir:
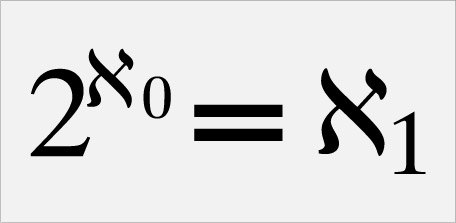
Figura. 5. La relación entre la cardinalidad de los Naturales y los Reales.
Y dejaré una última pregunta, que es una GRAN pregunta. Si hay estos dos infinitos y el primero es menor que el segundo, ¿Hay algún infinito intermedio? Esta pregunta, esta gran incógnita fue la más importante planteada por el gran matemático David Hilbert en el segundo congreso mundial de Matemáticas en París del año 1900. El nombre de esta gran hipótesis es “La hipótesis del Continuo de Cantor”, creada por el matemático Alemán Georg Cantor, que la formuló con implicaciones cataclísmicas para el mundo de la Lógica, las Matemáticas en sí y la Filosofía de la Ciencia.
Referencias
http://www.uv.es/ivorra/Libros/Logica.pdf
https://es.wikipedia.org/wiki/N%C3%BAmero_transfinito
http://philsci-archive.pitt.edu/13103/1/Cantor_Presentacion.pdf
Grandes temas de la matemática: Capítulo 13: Infinito
https://www.youtube.com/watch?v=TUFQKN5mIWM&ab_channel=Derivando
¿Cuántos Infinitos Existen? ∞ El Teorema de Cantor
Infinity is bigger than you think - Numberphile
Ficha del autor
Luis Leñero Elu: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Estudió Matemáticas en la Facultad de Ciencias de la UNAM. Es compositor, maestro y fundador del Instituto del Juego. Se ha dedicado a la enseñanza y la comunicación educativa aplicando tecnologías y gamificación en diversos ámbitos.



