
Tres tipos de lenguajes se utilizan para describir algo de la obra pictórica de Remedios Varo y relacionarla con su intuición físico-matemática: el lenguaje natural para describir el contenido de un catálogo de pinturas como si se tratara de un texto de mecánica, el lenguaje técnico de la física para analizar detalles de los cuadros Fenómeno de ingravidez y Creación de las aves y el lenguaje formal de las matemáticas para identificar las curvas cónicas que componen las trayectorias de una pelota manejada por El malabarista.
Hasta donde sabemos, Remedios Varo ni estudió física ni matemáticas; sin embargo, muchos de sus cuadros son evidencias de gran valor estético de una intuición muy original acerca del significado e importancia de diversos conceptos y procedimientos característicos de estas ramas del conocimiento científico.
El artículo consta de tres secciones, cada una de las cuales corresponde a un nivel de desarrollo en cuanto a la conjunción del lenguaje icónico con tres tipos de lenguajes, el natural que en este caso es el español, el técnico de la física y el formal de la matemática. Se trata de describir en términos físico-matemáticos diagramas que ilustran detalles observados en algunos cuadros de la pintora. Para mayor información, ver el libro La física en la obra pictórica de Remedios Varo.
Lenguajes icónico y natural
En un primer nivel de desarrollo empleo el lenguaje natural para describir la composición de un catálogo que comprende cuadros ordenados en las secciones que podrían ser las de un libro de mecánica: Los objetos, los seres y las fuerzas en la obra de Remedios Varo. A continuación, en la Tabla I indico los títulos de cada uno de los capítulos de ese libro inédito e incluyo los nombres de los cuadros que formarían parte de ese catálogo imaginario.

Tabla I. Contenido de un posible libro de mecánica: Los objetos, los seres y las fuerzas en la obra de Remedios Varo.
Lenguajes icónico y técnico
En un segundo nivel de desarrollo, describo con ayuda de diagramas algunos detalles de interés físico-matemático que me llaman la atención en dos cuadros de Remedios Varo: Fenómeno de ingravidez (CAT 359) y Creación de las aves (CAT 171).
Fenómeno de ingravidez
En la parte central del cuadro un astrónomo parece guiar la escapatoria de la Tierra junto con la Luna; ambos cuerpos celestes flotan en condiciones de ingravidez. Sin embargo, techo, piso, paredes y ventana forman dos sistemas de referencia que coexisten superpuestos con distintos orígenes y orientaciones. Para pasar del sistema S al sistema S´ hay que hacer una rotación del ángulo α (Figura 1).
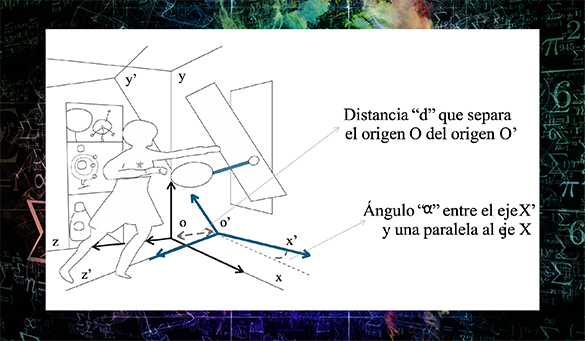
Diagrama 1. Se muestra la rotación de los ejes (X´, Y´, Z´) del sistema S´ respecto de los ejes (X, Y, Z) del sistema S, en el cuadro Fenómeno de ingravidez. Los dibujos y las letras han sido colocados por el autor como apoyo a la representación esquemática de un detalle del cuadro. Fuente: Figura 2.2 del libro La física en la obra pictórica de Remedios Varo, p. 35.
Consideremos que el cuadro representa el escenario geométrico en cuatro dimensiones en el cual se mueven la Tierra y la Luna. El evento que describe el cuadro – flotación de dos astros - ocurre en cierto momento (instante de tiempo t) y lugar (posición definida por las coordenadas en los ejes X, Y y Z). Las correspondientes coordenadas espaciotemporales de la mancuerna Tierra-Lun quedarán descritas en el sistema S por la cuarteta (x, y, z, ct) y en el sistema S´ por la cuarteta (x´, y´, z´, ct´), donde c es la velocidad de la luz. Si el sistema S’ se aleja del sistema S con una velocidad v cercana a la velocidad de la luz (c), las relaciones que permiten pasar de las cuatro coordenadas espaciotemporales en S a las correspondientes coordenadas en S´ constituyen las llamadas transformaciones de Lorentz, una de cuyas consecuencias es que los intervalos de tiempo se alargan y las distancias se acortan.
A lo mejor, el astrónomo del cuadro conoce y controla estas transformaciones porque la intuición físico-matemática de la pintora ha expresado el hecho de que una rotación en el espacio de cuatro dimensiones corresponde, desde el punto de vista de la teoría de la relatividad especial, a las transformaciones de Lorentz.
Creación de las aves
Un ser con aspecto de lechuza y cuerpo emplumado maneja tres procesos que corresponden a otros tantos tipos de radiaciones: una radiación atraviesa un prisma e incide sobre un papel, otra radiación pasa por un alambique y se deposita en una paleta, y una tercera radiación emana de un corazón en forma de violín y llega a un pincel (Figura 2). En el cuadro Creación de las aves, la intuición físico-matemática de la pintora nos presenta una especie de efecto fotoeléctrico.
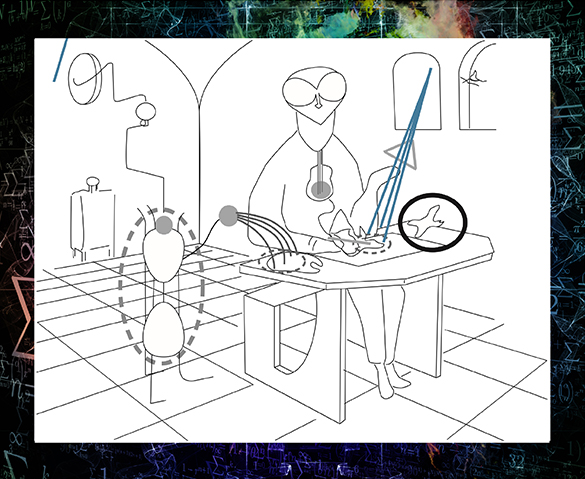
Diagrama 2. Representación esquemática de un detalle del cuadro Creación de las aves. Fuente: Figura 2.3, del libro La física en la obra pictórica de Remedios Varo, p.39
El efecto fotoeléctrico consiste en que una radiación luminosa de cierta energía (un haz de fotones) incide sobre la superficie de un metal y provoca la salida de electrones que constituyen una corriente eléctrica. Sin embargo, las características de las radiaciones que aparecen en el cuadro escapan al conocimiento actual de la física moderna por las razones siguientes: el primer proceso señala el paso de la luz por el prisma, pero los rayos no cambian de dirección; es decir, no se refractan. El segundo proceso sugiere que el alambique transforma la radiación incidente en gotas líquidas de tres pigmentos con los colores primarios. El tercer proceso presenta el impacto de una radiación en un papel donde el dibujo de un ave se llena de color, cobra vida y vuela. Esto es algo así como una especie de efecto foto-acústico-mecánico-cromático-biológico donde, en lugar de que los fotones provoquen la salida de una corriente de electrones, tres tipos de radiaciones dan vida al dibujo de un ave.
Lenguajes icónico y formal
En un tercer nivel de desarrollo, la descripción en el lenguaje técnico de la física se amplía con el análisis matemático de la trayectoria de una partícula: la pelota que maneja el malabarista del cuadro “El malabarista” (CAT 154). Supondré que el objeto en movimiento es una partícula puntual sin estructura y que no se trata de muchas pelotas en movimiento simultáneo, sino de una sola que ocupa diecinueve posiciones sucesivas en distintos instantes de tiempo. Además, como primera aproximación, consideraré que ese movimiento ocurre en el plano de la pintura, como proyección en dos dimensiones de un movimiento que en la realidad es tridimensional. Las posiciones de la pelota me servirán para averiguar cuáles son las curvas matemáticas que corresponden a las trayectorias pintadas: son como las mediciones experimentales de un observador (Figura 3).
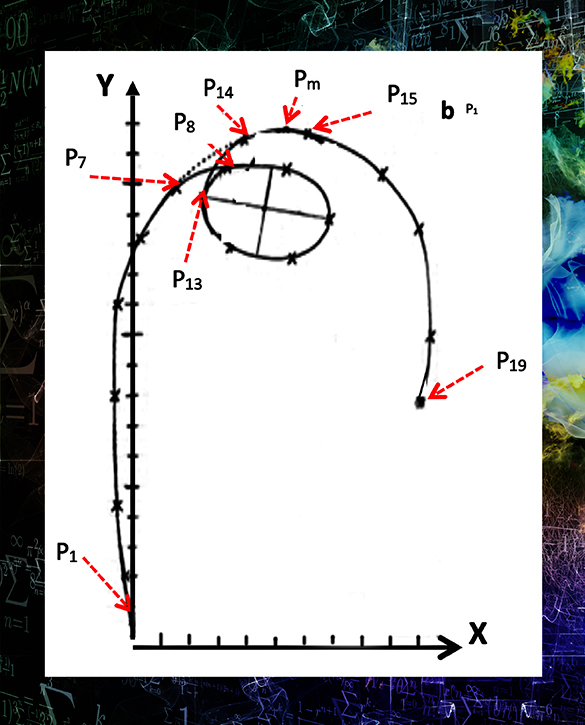
Diagrama 3. Representación en el plano cartesiano (ejes X e Y) de las diecinueve posiciones sucesivas de una pelota cuyo movimiento se inicia en la posición P1 y termina en la posición P19.
Suponiendo que la pelota del malabarista está sujeta a la fuerza de gravedad, que es una fuerza central conservativa, la trayectoria correspondiente será una curva cónica de energía y de excentricidad . En esta ecuación, el término de energía contiene el conocimiento físico acerca de la trayectoria mientras que la excentricidad está asociada con las características geométricas de la trayectoria. El valor de la excentricidad determina de qué cónica se trata: cuando ε = 1 es una parábola, si ε < 1 es una elipse, si ε > 1 es una hipérbola y si ε = 0 es un círculo.
El análisis matemático del movimiento de la pelota del malabarista comprende tres etapas: primero, meedir en la pantalla de la computadora los valores numéricos de las coordenadas de cada punto de las tres trayectorias del diagrama de la Figura 3: T1 (de P1 a P7), T2 (de P8 a P13) y T3 (de P14 a P19). Después, hacer el ajuste de mínimos cuadrados para determinar la forma de la ecuación de la curva correspondiente a cada trayectoria. Finalmente, determinar los valores de la excentricidad y de la energía , los cuales se comparan en la Tabla II con los valores teóricos que representan a cada curva cónica.
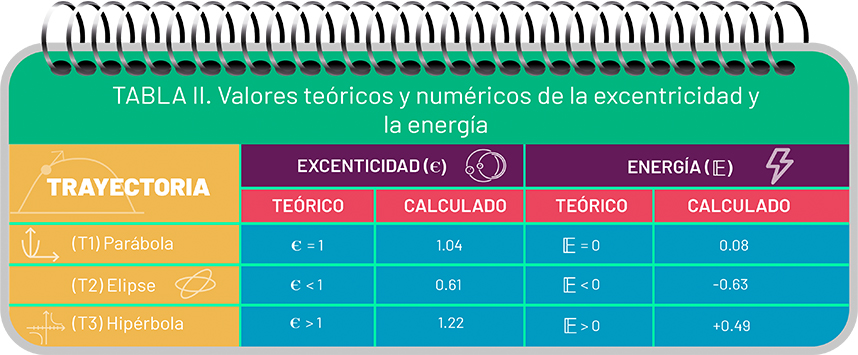
Es sorprendente que los valores de la energía y la excentricidad obtenidos a partir del análisis de las trayectorias de la pelota concuerden en buena medida con los valores teóricos que deben tener las correspondientes curvas cónicas. Por supuesto, el cuadro para nada nos sugiere cómo es que la pelota del malabarista pasa de la parábola a la elipse (transición de P7 a P8) y de la elipse a la hipérbola (transición de P13 a P14). Por otra parte, hay que recordar que la pintura es la representación en un plano de un movimiento que ocurre en tres dimensiones y transcurre en el tiempo.
Nuevamente la intuición físico-matemática de Remedios Varo nos da en este cuadro, seguramente sin haberlo pretendido, una lección de geometría analítica, cálculo numérico y descripción física del movimiento.
Muchos cuadros de Remedios Varo pueden conectarse con modelos y circunstancias características del estudio del movimiento, la energía, el calor, la luz, la electricidad, el magnetismo. Probablemente Remedios Varo no pretendió mostrar sus ideas acerca del mundo físico ni hacer cálculos matemáticos para planear y pintar sus cuadros. No se limitó a lo que comúnmente comprende la ciencia, la trascendió poéticamente. Son muestras ejemplares de su gran intuición físico - matemática donde lo improbable es factible. Los textos oficiales lo calificarían de imposible, pero ella les ha dado vida en nuestra imaginación.
Referencias
Barojas Weber, Jorge (2019). La física en la obra pictórica de Remedios Varo. Colección Investigación. Universidad Autónoma de Aguascalientes. ISBN 978-607-8714-02-3.
Ficha del autor
Jorge Barojas Weber: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Profesor del Departamento de Física de la Facultad de Ciencias y tutor en el Doctorado en Ciencias de la Administración (línea de investigación en administración del conocimiento), ambas de la UNAM. Actualmente es investigador adscrito a la Unidad Académica del ILCE.



