
La presentación de los trabajos de tres niñas de primaria que realizaron dibujos y esculturas con inspiración geométrica, sirve de introducción para analizar algunos aspectos de la participación de las mujeres en la enseñanza, estudio y aplicación de las matemáticas.
Durante muchos años los accesos a la educación y a la investigación científica han estado limitados y hasta prohibidos a las mujeres, especialmente en relación con el estudio de las matemáticas. Esto ha variado en intensidad y consecuencias a lo largo de la historia de la humanidad, desde tiempos en que la matemática griega Hipatia de Alejandría fue asesinada por una secta fanática de cristianos, hasta la época moderna con casos como el de Emmy Noether (Figuras 1a y 1b).
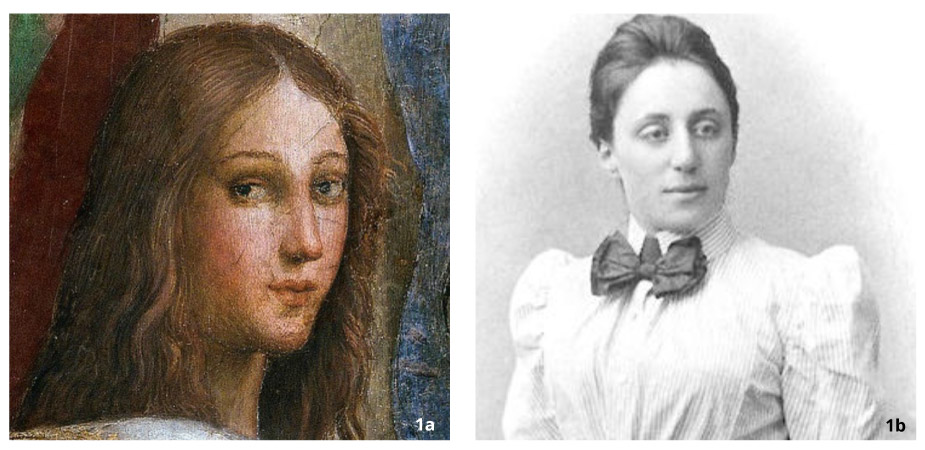
Figura 1. Dos grandes matemáticas: (a) Hipatia de Alejandría (360-415) y (b) Emmy Noether (1882-1935).
La genial matemática alemana necesitó de un permiso especial para poder asistir a clases de doctorado, luego cuando ya había obtenido dicho grado se le autorizó que diera clases, pero sin recibir salario. Por ser de origen judío tuvo que emigrar a los Estados Unidos y en 1934 comenzó a dar clases en el Instituto de Estudios Avanzados de Princeton; sin embargo, no se le ofreció un puesto permanente en la Universidad de Princeton por ser una universidad de hombres, donde no se admitía a ninguna mujer. Finalmente fue aceptada en una pequeña universidad privada para mujeres.
Lo que ha sido constante es el prejuicio casi universal de que las mujeres no tienen aptitudes para entender, desarrollar y aplicar las matemáticas. Esta injustificada regla de discriminación se ha aplicado a todas las edades, con mayor desvergüenza en la infancia y adolescencia.
Como elocuente desmentido a todo lo anterior, les presento lo que dijeron y mostraron tres niñas de primaria que participaron el semestre pasado en el proyecto colaborativo El espacio y el entorno: Geométricos, organizado por el equipo de RedEscolar del ILCE. Ciertamente, estas niñas gozaron al vivir la geometría y lo expresaron con alegría (Figuras 2a, 2b y 2c). La Tabla I contiene los datos y lo que explicaron estas creadoras de geometría.

Figura 2. Las formas geométricas y el arte según tres niñas de primaria: (2a) dibujo de Sofía; (2b) escultura de Ángeles y (2c) dibujo de Xóchitl.

El proyecto El espacio y el entorno: Geométricos se diseñó en RedEscolar (Figura 3) como un apoyo didáctico para maestros con el fin de presentarle opciones de cómo y para qué cubrir los contenidos curriculares de la asignatura de Matemáticas de 5º y 6º grado de Primaria, en los bloques correspondientes al tema “Forma, espacio y medida". La intención era conectar el estudio de la geometría con asignaturas tales como ciencias naturales, español, historia y educación artística.

El proyecto colaborativo en consideración persiguió los siguientes propósitos para los alumnos:
- Analizar las propiedades y características de las figuras geométricas.
- Identificar figuras geométricas en distintos entornos.
- Reconocer y aplicar ideas y relaciones geométricas vinculadas con otras asignaturas.
- Desarrollar habilidades relacionadas con el manejo de información matemática.
- Elaborar materiales de divulgación sobre las relaciones y conceptos geométricos.
- Hacer uso de las herramientas de comunicación y colaboración para la socialización de los aprendizajes.
El procedimiento consistió en que los alumnos formaran cinco equipos (matemáticos, historiadores, escritores, artistas y científicos) y que durante nueve semanas prepararan distintos productos bajo la dirección de su maestro. Todos estos productos se relacionaron con la geometría: los matemáticos propusieron un juego, los historiadores una línea del tiempo, los escritores un relato, los artistas un dibujo o escultura y los científicos una galería fotográfica. Esto ocurrió mientras continuaban las clases por televisión y en casa, dentro de las condiciones de pandemia que ha vivido el país.
Los tres productos mostrados con anterioridad en las Figuras 2a, 2b y 2c se refieren únicamente al equipo de artistas y son resultado de un extraordinario trabajo de motivación y orientación interdisciplinaria por parte de los profesores; además, muestran que las escuelas donde estudian Sofía, Ángeles y Xóchitl, pertenecen a la categoría de escuela-festival creativo porque ahí aprender implica crear y compartir con alegría y satisfacción.
En forma esquemática podemos hablar de tres tipos de escuelas; la escuela-cuartel punitivo en la cual se ordena, premia y castiga; la escuela-fábrica productiva donde se prepara para el mercado competitivo, y la escuela-festival creativo en la que se gozan, comparten enseñanzas y aprendizajes. En realidad, toda institución educativa tiene algo de estos tres tipos de escuelas porque, entre otras cosas: se cumplen con planes y programas de estudio, hay calendarios con fechas y metas; se forman, actualizan y evalúan maestros; se elaboran materiales didácticos y se utilizan herramientas tecnológicas; se presentan exámenes y se dejan tareas y, finalmente, se aplican procesos de selección y se otorgan diplomas, títulos o certificados.
Lo importante y significativo es la proporción con la cual intervienen los tres tipos de escuelas antes descritos. En la base del triángulo de los tipos de escuelas (Figura 4) tenemos a las escuelas tradicionales donde se ejerce dominio y control de contenidos y enfoques por conducto de maestros, planes y programas de estudio, libros de texto, exámenes y calificaciones. En la región intermedia las escuelas buscan modernizarse en cuanto a metodologías y usos de tecnología, con dificultades para establecer un adecuado balance entre información y formación. En el ápice del triángulo están las escuelas creativas e innovadoras caracterizadas por una dinámica de participación guiada en la que los estudiantes construyen sus aprendizajes. Para pasar de una región a otra de dicho triángulo deben vencerse ciertas barreras para lograr cambios tecnológicos y cognitivos.
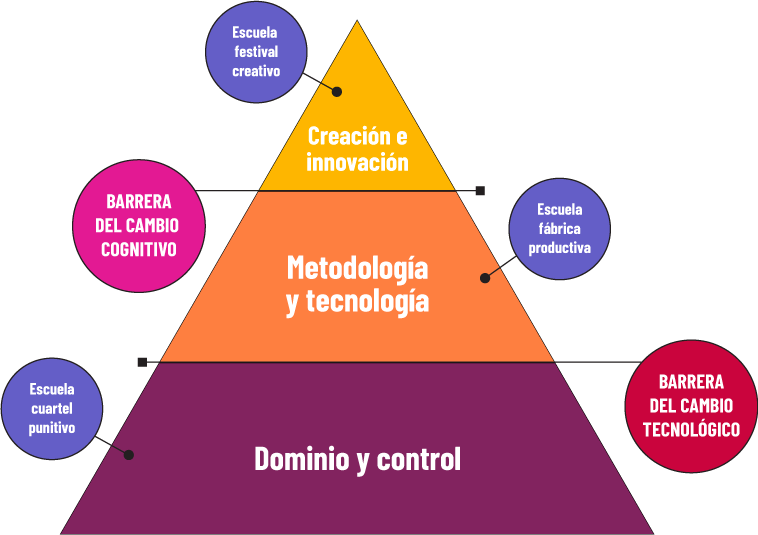
Figura 4. Triángulo de los tipos de escuelas
Como elemento de inspiración, con el fin de tener ideas para pasar la barrera del cambio cognitivo, conviene referirnos al matemático mexicano Alberto Barajas Celis, quien ha dicho: “Sí, creo que las matemáticas son una de las creaciones más bellas del espíritu humano. (Si me pusieran un detector de mentiras indicaría que estoy mintiendo. No pienso que sea una de las más bellas. Es, la más bella.)”
En lo que sigue transcribo tres fragmentos de la conferencia del Dr. Barajas (Figura 5): En el principio era la geometría. (Tomada del libro Alberto Barajas. Su oratoria, sus matemáticas y sus enseñanzas.)

Figura 5. Alberto Barajas Celis (1913-2004)
Cuando al mismo Newton le preguntaron cómo había descubierto la ley de la gravitación universal, contestó con una frase de enamorado. Pensando en ella de día y de noche.
La naturaleza se ha encargado de enseñarnos geometría durante millones de años. Nuestra capacidad para percibir imágenes, archivarlas en la memoria y ordenarlas en el espacio y el tiempo es increíble. Bien, si ya sabemos geometría al nacer ¿qué fue lo que inventaron los griegos? Los griegos descubrieron que este mundo riquísimo de imágenes no es un caos, no está regido por la arbitrariedad ni la locura. Las figuras tienen sus reglas de juego, y éstas son accesibles a la razón humana. Desde los griegos el universo se goza con la mirada y con la inteligencia. Que el universo tiene sentido es uno de los descubrimientos más voluptuosos que ha hecho el ser humano.
Desgraciadamente la comunidad científica no siempre ha manifestado haber entendido que el elocuente y generoso pensamiento de Barajas se aplica a una visión de las matemáticas que debe ser compartida con todo ser humano. En muchas actividades se ha olvidado que el género femenino es algo más que la mitad de la humanidad y que todas, niñas, jóvenes y adultas, todas tienen derecho a educarse. Aquí lo menciono en relación con las oportunidades que tienen las mujeres para desarrollar y aplicar su talento, haciendo o utilizando matemáticas.
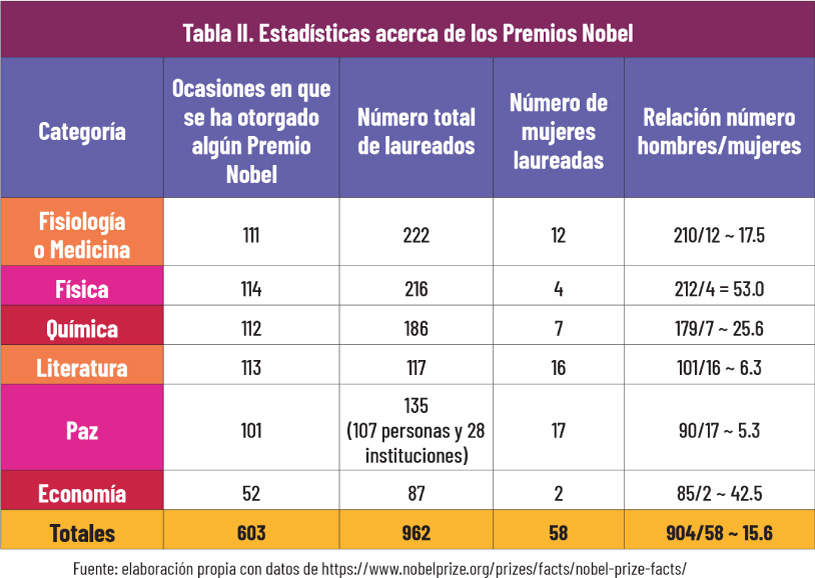
Una comparación interesante es el número de mujeres que han recibido el Premio Nobel. Salvo en los Premios de Literatura y Paz, de una manera o de otra se han utilizado matemáticas en la elaboración de los trabajos que han recibido tal reconocimiento en Fisiología o Medicina, Física, Química y Economía.
Conviene observar que en 2020 el Premio Nobel se concedió a 7 hombres y a 4 mujeres, la relación más baja obtenida hasta ahora porque el número de mujeres resultó ser casi la mitad del número de hombres (4/7 = 0.57).
Incidentalmente Alfred Nobel excluyó en su testamento a las Matemáticas. Sin embargo, algo equivalente al Premio Nobel de Matemáticas es la Medalla Fields, la cual, a partir de 1936, se otorga cada cuatro años a matemáticos menores de 40 años. La matemática iraní Maryam Mirzakhani, profesora de la Universidad de Stanford, fue la primera mujer en recibir esta medalla en 2014.
En la actualidad existen muchos programas para promover el interés por aprender matemáticas y dar a conocer resultados de investigaciones acerca de su enseñanza. También hay una muy amplia gama de recursos didácticos para mejor el rendimiento escolar en prácticamente todos los niveles, desde el preescolar hasta el posgrado. Además, se han puesto en operación proyectos especiales asociados a museos y clubes de ciencia o patrocinados por instituciones tales como la Academia Mexicana de Ciencias, la Sociedad Matemática Mexicana, el Departamento de Matemática Educativa del CINVESTAV, así como la Facultad de Ciencias y el Instituto de Matemáticas de la UNAM. Algunas de estas actividades están especialmente orientadas para apoyar a las mujeres en el estudio y aplicación de las matemáticas. Concretamos lo anterior con tres referencias a productos generados por el ILCE:
(1) Los laboratorios virtuales de matemáticas desarrollados por el Instituto Galileo de Innovación Educativa, descritos con claridad en el capítulo 6. Desarrollando el interés por las matemáticas, del libro Educación para el cambio de Enrique Calderón Alzati.
(2) La colección La reina de las ciencias, que forma parte de la Biblioteca Digital, cubre prácticamente todas las ramas de las matemáticas y contiene como un centenar de contribuciones de los matemáticos más importantes, de Arquímedes y Euclides a nuestros días, traducidas al español por Emilio Méndez Pinto, con algunos artículos propios. En especial, destacamos los artículos ¿Qué son las matemáticas?, Cómo escribir Matemáticas y Emmy Noether, descritos en las Referencias.
(3) Artículos publicados por la Revista "Nueva educación latinoamericana”: la transcripción de la conferencia de Cédric Villani (Medalla Fields de 2010) ¿Por qué las matemáticas son tan sexis? publicada en el primer número de julio, y el artículo de Luis Leñero El poder de la imaginación, publicado en el segundo número de septiembre. (Acceso en https://revista.ilce.edu.mx/)
Referencias
Calderón Alzati, E. (2019). Educación para el cambio. México: ILCE Editorial.
Courant R. y Robbins H. (2017). ¿Qué son las matemáticas? Biblioteca Digital del ILCE. Obtenido de http://bibliotecadigital.ilce.edu.mx/Colecciones/ReinaCiencias/_docs/Que_son_las_matematicas-Courant.pdf
Halmos P. (2017). Cómo escribir Matemáticas. Biblioteca Digital del ILCE. Obtenido de http://bibliotecadigital.ilce.edu.mx/Colecciones/ReinaCiencias/_docs/Como_escribir_matematicas-Paul_Halmos.pdf
Newmann-Lara, V. (2010). Alberto Barajas. Su oratoria, sus matemáticas y sus enseñanzas. Sociedad Matemática Mexicana, Instituto de Matemáticas, Facultad de Ciencias, México: UNAM.
Weyl H. (2017) Emmy Noether. Biblioteca Digital del ILCE. Obtenido de
http://bibliotecadigital.ilce.edu.mx/Colecciones/ReinaCiencias/_docs/EmmyNoether.pdf
Ficha del autor
Jorge Barojas Weber: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Profesor del Departamento de Física de la Facultad de Ciencias y tutor en el Doctorado en Ciencias de la Administración (línea de investigación en administración del conocimiento), ambas de la UNAM. Actualmente es investigador adscrito a la Unidad Académica del ILCE.



