Alan Turing sentó las bases del desarrollo de las computadoras, gracias a la concepción de la máquina que lleva su nombre. Como muchas de las innovaciones tecnológicas a través de la historia, surge en el contexto de la guerra y sus aplicaciones al día de hoy son impresionantes.
En este artículo se reconoce la capacidad de este connotado científico de emular en una máquina, las capacidades de cálculo matemático del cerebro de animales y humanos. Sin duda, uno de los precursores de los avances tecnológicos de la humanidad, que no recibió en vida el lugar que merecía por su enorme talento.
Hoy en día las computadoras electrónicas con todas sus variantes, incluyendo las tabletas, los celulares y toda una variedad de dispositivos que han hecho posible el funcionamiento de robots y de aparatos automáticos de alta complejidad, son utilizados por la industria y por millones de personas en todo el planeta. Sin embargo hoy solo muy pocas personas saben o han oído hablar del investigador que hizo posible todo esto.
Brillante matemático y precursor de las ciencias de la computación
Alan Mathison Turing fue un matemático inglés quien en 1936 estableció la tesis de que se puede diseñar una máquina capaz de resolver cualquier problema matemático, siempre y cuando se cumplan 3 condiciones: uno, que se puedan representar sus elementos de manera digital; dos, que la máquina haga operaciones básicas y tres, que se pueda utilizar un programa o listado de cómo aplicar dichas operaciones. En los años siguientes un buen número de científicos fracasaron tratando de encontrar un problema matemático que esta máquina hipotética no pudiera resolver mediante una secuencia finita de las operaciones definidas por Alan Turing. No lo lograron.

Figura 1. El matemático inglés Alan Turing (1912-1954).

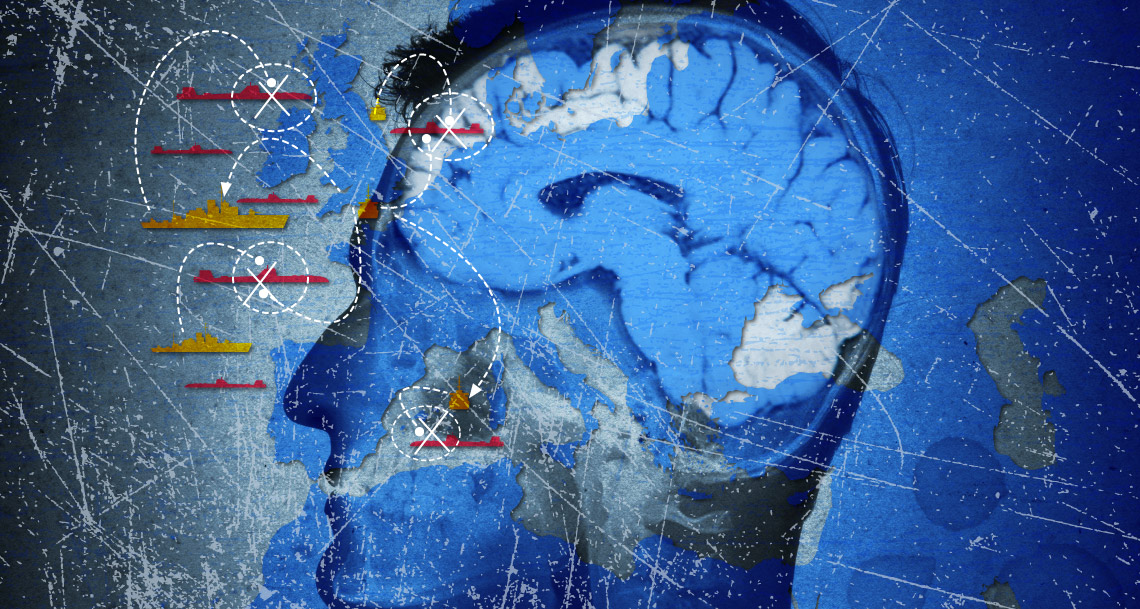
Figura 2. Máquina de Turing, para descifrar el código “Enigma” de los alemanes
Luego del inicio de la Segunda Guerra Mundial y de la campaña relámpago realizada por los nazis que les permitió ocupar los Países Bajos y derrotar a los franceses e ingleses en Normandía, Hitler ordenó a su ejército y a su flota de submarinos sitiar a Inglaterra para luego invadirla.
Lo anterior provocó que el Servicio de Inteligencia Inglés le encargara a Alan Turing en 1941 la construcción de una máquina que les permitiera descifrar el código “Enigma” que los alemanes estaban utilizando para comunicar a sus submarinos la posición de los buques aliados. El objetivo era que los submarinos hundieran a los buques antes de que llegaran a los puertos ingleses para descargar alimentos, medicinas y armas en Inglaterra.
Luego de varios meses de trabajo, la máquina diseñada y construida por Turing logró descifrar los mensajes, de manera que cuando los barcos cambiaron su ruta se logró eliminar el bloqueo contra Inglaterra. Antes de que terminara la segunda guerra mundial, y siguiendo los pasos de Turing, los norteamericanos lograron construir la primera computadora de propósito general, a la que le dieron el nombre de “ENIAC” (Electronic Numerical Integrator And Computer). El éxito de esta máquina, primera en la solución de complejos problemas de matemáticas y física y luego clave en la solución de un amplia y creciente gama de problemas, se debió en gran parte a otro gran matemático: Kurt Gödel. La aportación de este matemático hizo posible que las computadoras comenzaran a operar también con las letras del alfabeto y con diversos signos, tanto de puntuación como matemáticos, ampliando enormemente sus posibilidades de utilización mediante la transformación de las palabras en secuencias numéricas.
Alan Turing nunca fue galardonado ni reconocido por su gran invento, en tanto éste era considerado un secreto militar. Terminó su vida suicidándose, como respuesta a un juicio realizado por su propio gobierno: fue condenado a la carcel por el terrible delito de ser homosexual. Todo esto ocurrió algún tiempo antes de que las computadoras comenzaran a tener éxito a nivel internacional.
¿"Máquinas de Turing" en la naturaleza?
Lo que Turing nunca pudo imaginar es que todos los cerebros de los animales, son en realidad Máquinas de Turing, lo cual podría parecer una afirmación absurda. Sin embargo, ¿cómo podemos explicar que las abejas sean capaces de construir las estructuras geométricas que utilizan para almacenar la miel que producen? Y de la misma manera ¿cómo explicar la existencia de las telarañas, construidas por las arañas para capturar insectos que le sirvan para alimentarse?

Figura 3. Panal construido por abejas
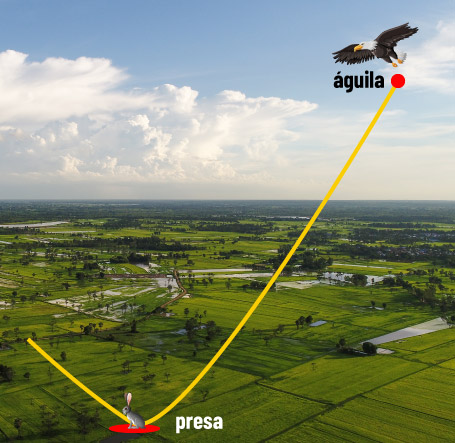
Figura 4. Trayectoria de águila para capturar una presa
De manera similar podemos mencionar el caso de las águilas y en general de las aves de caza. Cuando una de estas aves observa una posible presa desde centenares de metros de distancia y altura, debe estimar si podrá levantarla sin estrellarse contra un árbol o una roca, para luego lanzarse sobre ella siguiendo una trayectoria mostrada en la figura (4). Todo este proceso implica una serie de cálculos que realiza el cerebro del ave, sin que ésta sea conciente de ello.
De la misma manera podemos pensar en todas las especies de animales mamíferos, entre las cuales podemos seleccionar como un último ejemplo el de los chimpancés o de los orangutanes. Normalmente se mueven en la selva saltando de un árbol a otro, de manera que sus cerebros demuestran ser capaces de estimar las distancias que pueden saltar, sin riesgo de caer por no brincar con la suficiente energía. Así muestran sólo una parte de sus habilidades matemáticas, dado que antes de hacer el salto deben asegurarse de que podrán alcanzar la siguiente rama en otro árbol y así, sucesivamente brincar de rama en rama para llegar a un destino que puede estar a decenas o centenas de metros.
El cerebro humano y el cálculo
En el caso de los seres humanos podemos pensar en el billar, en el que claramente el cerebro de los jugadores está continuamente realizando cálculos que le permitan realizar complicadas jugadas. El ejemplo mostrado en la figura (5) corresponde a una carambola “de tres bandas” según la cual la pelota blanca pegará a la pelota amarilla después de rebotar tres veces en las bandas laterales de la mesa de billar. El que un jugador logre hacer lo anterior no necesariamente se debe a sus estudios formales que le permiten hacer cálculos complicados, sino a su experiencia en el juego obtenida después de muchas horas de práctica.
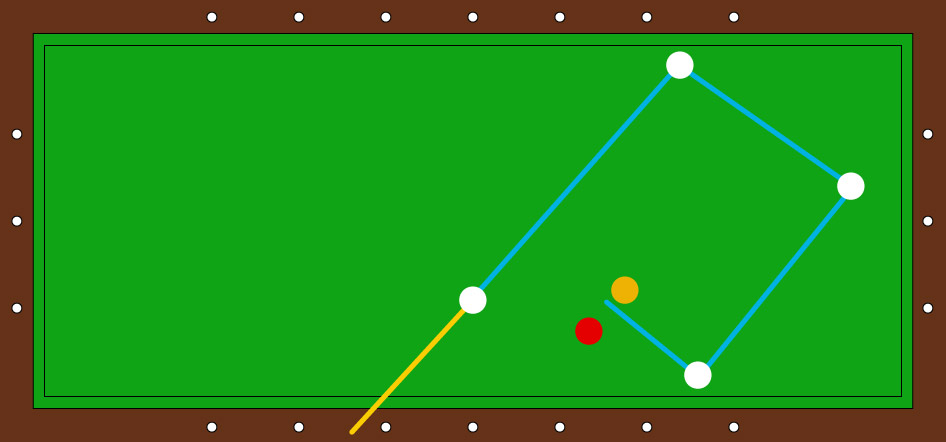
Figura 5. Carambola de tres bandas en mesa de billar
Al analizar estos hechos no debiera sorprendernos que en todos los deportes que se juegan con pelotas o balones sea posible observar movimientos extraordinarios que realizan los jugadores, por ejemplo: meter un gol en el caso del fútbol, atrapar una pelota en el caso del béisbol o de contestar un tiro de un jugador contrario en el del Voleibol. En estos casos los jugadores nunca son concientes de los cálculos realizados por sus cerebros: su aprendizaje se reduce a los entrenamientos previos, sin que en ellos se incluyan aspectos matemáticos.

Figura 6. Atrapada de pelota antes de tocar el suelo.

Figura 7. Plática de cafetería y cálculos matemáticos
Los seres humanos utilizamos la capacidad matemática de nuestros cerebros no solo en los deportes sino en todas las actividades que realizamos. En la figura (7) se aprecia a dos jóvenes sosteniendo una plática seguramente agradable mientras toman café. Es bastante claro que ellos dedican su atención a la conversación misma; sin embargo, pensemos en los movimientos de sus manos sosteniendo las tazas de café. Por su parte, la chica sujeta la taza con una mano, mientras con la otra mantiene el plato donde colocará la taza, después de beber un trago de café. Mientras esto sucede, su cerebro está calculando las posiciones de la taza y del plato, de manera que cuando ella decida colocar la taza sobre el plato, quede ubicada en su centro y con una inclinación idéntica en ambas piezas. Esto nada tiene de trivial, es geometría en tres dimensiones.
Desde luego existe una gran diferencia entre las capacidades matemáticas del cerebro humano y las de los animales, la cual podemos explicar de la manera siguiente: los animales nacen con algoritmos específicos ”cableados” en los genes de sus cerebros, los cuales definen las actividades exclusivas de carácter matemático que podrán realizar los animales a lo largo de sus vidas. En el caso de los insectos se trata de un solo algoritmo de naturaleza sencilla y en el caso de los animales superiores los algoritmos son más complejos y presentan algunas variantes, mientras que en el caso de los seres humanos el cerebro tiene una capacidad ilimitada de crear sus propios algoritmos en la medida que ello se hace necesario.
También es posible que la máquina de Turing que opera en el cerebro humano tenga una mayor capacidad de cómputo, dado que el cerebro de los seres humanos es significativamente más grande que el de los animales mencionados en este artículo.
Ficha del autor
Enrique Calderón Alzati: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Doctor en Ciencias de la Computación y la Información por la Universidad de Pennsylvania. Autor de varios libros, articulista de La Jornada. Actualmente es Director General del Instituto Latinoamericano de la Comunicación Educativa (ILCE).



