
A mi mamá, Margarita Pinto Gil, cuyo amor y apoyo hicieron posible este proyecto y muchas otras cosas más.
Beauty in mathematics is seeing the truth without effort.
G. Pólya
A good part of the program of elementary or secondary schools is very arid and technical, and you may never have had the luck to see how mathematics can be beautiful.
S. Lang, The Beauty of Doing Mathematics
Abunda evidencia sobre el analfabetismo matemático a nivel mundial. Como una instancia de ello, se recurre a los indicadores del Departamento de Asuntos Económicos y Sociales de las Naciones Unidas sobre las tasas de competencia en lectura y matemáticas en niños y adolescentes a nivel global (2015).[2] Estos indicadores muestran que, a nivel global, el 56% de los niños y adolescentes carece de una competencia mínima en matemáticas. Para la región de América Latina y el Caribe, el 52% de los niños y adolescentes carece de dicha competencia mínima.
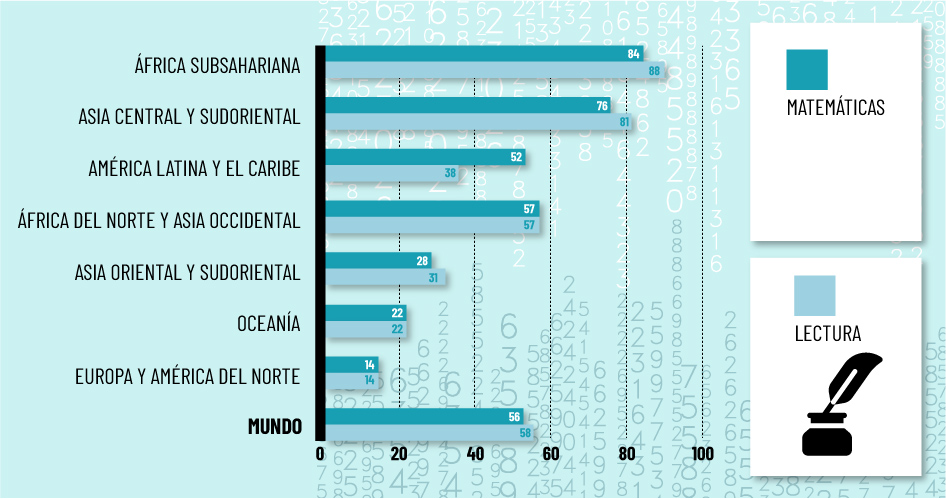
Gráfica 1. Porcentaje de niños y adolescentes que no alcanzan una competencia mínima en lectura y matemáticas, 2015 (promedio). Fuente: Departamento de Asuntos Económicos y Sociales de las Naciones Unidas.
Ante esta situación, los expertos –incluidos los del Departamento de Asuntos Económicos y Sociales de las Naciones Unidas– suelen proponer dos soluciones: mejorar la calidad de la educación y universalizar el acceso a dicha educación. Desde sus inicios, La Reina de las Ciencias ha puesto sus baterías en la segunda solución.
Breve historia de la colección La Reina de las Ciencias
Fue por la lectura de algunos filósofos (Hume, Kant, Peirce) que, proponiéndoselo o no, desarrollaron una filosofía de las matemáticas (o algo muy cercano a ello), que al creador de la colección y traductor de las obras Emilio Méndez Pinto empezó a interesarse seriamente el estudio de la filosofía de las matemáticas, y no sólo por el lado de los filósofos, sino también por el lado de los matemáticos: si, por ejemplo, Kant escribió sobre el quehacer matemático, ¿qué dijeron un Poincaré o un Hilbert o un Weyl al respecto? El estudio de la filosofía de las matemáticas por el lado de los matemáticos lo llevó, pronto, al estudio de las matemáticas propiamente dichas. Fue entonces cuando leyó las Lecciones sobre matemáticas elementales de Lagrange, los Elementos del Álgebra de Euler, entre otras obras clásicas de la literatura matemática.
Leyó a Lagrange y a Euler en inglés (para el caso de Lagrange, la traducción de T. McCormack de 1901; para el caso de Euler, la traducción de J. Hewlett de 1822) porque, en ese entonces, ninguna de dichas obras estaba traducida al español. Surgió la pregunta en él –visto en retrospectiva e ingenuamente– si sus casos eran la norma o la excepción. Resultaron ser la norma, y no sólo en su tipo: descubriendo decenas de obras clásicas[3] de lógica, de filosofía de las matemáticas, de lógica matemática, de filosofía de la lógica, de lógica filosófica, etc., imposibles de leer en español. Fue ante esto que se propuso la tarea de traducir al español y de divulgar la mayor cantidad posible de textos de matemáticas, filosofía de las matemáticas, etc., para la mayor cantidad posible de personas hispanohablantes. Y fue en la Biblioteca Digital del ILCE donde se pudo concretar esta tarea.
Sabiendo que el ILCE tenía una Biblioteca Digital y que en ella no había una colección dedicada exclusivamente a las matemáticas, hubo un acercamiento en 2012 y el ILCE estuvo interesado en el proyecto de divulgación.
En un principio, como una suerte de homenaje a Galileo, se sugirió el nombre de El alfabeto de Dios para la colección. Por razones de laicidad, la propuesta de nombre fue rechazada (visto en retrospectiva, atinadamente rechazada). Se sugirió entonces el nombre de La Reina de las Ciencias, ahora como una suerte de homenaje a Gauss, a quien se le atribuye la frase: “Las matemáticas son la reina de las ciencias”.[4] Una vez elegido el nombre, quedaba lo más importante: elegir qué obras serían parte de la colección. El creador de la colección decidió que las Lecciones sobre matemáticas elementales de Lagrange, los Elementos del Álgebra de Euler, y Ciencia e hipótesis, Ciencia y método, y El valor de la ciencia, de Poincaré, serían obras idóneas para inaugurarla. Con el paso del tiempo, las obras que se han ido traduciendo para la colección han pasado de ser libros a ser artículos académicos, y de ser sobre matemáticas (o ciencia en general, como en el caso de Poincaré) a ser también sobre filosofía de las matemáticas, filosofía de la ciencia, filosofía de la lógica, lógica matemática, etc., (con todas sus zonas limítrofes, parafraseando a Hempel).

Gráfica 1. Porcentaje de niños y adolescentes que no alcanzan una competencia mínima en lectura y matemáticas, 2015 (promedio). Fuente: Departamento de Asuntos Económicos y Sociales de las Naciones Unidas.
Hoy en día, en La Reina de las Ciencias cuenta con 114 obras traducidas al español[5] de matemáticos como Turing, Borel, Courant, Erdős, Lang, Halmos, Brouwer, Weierstrass, Dedekind, Cantor, Weyl, Cauchy, Boole, Arquímedes, Birkhoff, Laplace, Wiener, Skolem, Klein, Bourbaki, Hilbert, Hardy, Ramsey, Peano, Lebesgue, Gauss, Artin, Kronecker, Bernays, Galois, Von Neumann, Riemann, Newton, Kolmogórov, Cohen, y los ya mencionados Lagrange, Euler, y Poincaré, de lógicos como Gödel, Boolos, Kreisel, Curry, Kleene, Church, y Tarski, y de filósofos como Burgess, Bolzano, Goodman, Quine, Kripke, Russell, Benacerraf, Feferman, Frege, Putnam, Leibniz, Peirce, Hempel, Wang, Parsons, Carnap, y Whitehead. De estas 114 obras traducidas, 98 son inéditas en español.
A lo largo de su corta vida, La Reina de las Ciencias ha recibido el auspicio –normalmente, bajo la forma de conceder permisos de traducción y posterior publicación– de los filósofos Hilary Putnam, Paul Benacerraf, y Sally Sedgwick (quien otorgó los permisos de traducción y publicación de La concepción iterativa de conjunto, del gran George Boolos), del matemático Jürgen Elstrodt (quien permitió traducir y publicar en esta colección su magnífica biografía sobre Dirichlet), de las revistas académicas The Journal of Philosophy, The Philosophical Review, Notre Dame Journal of Formal Logic, The Journal of Symbolic Logic, Mind, The American Mathematical Monthly, Bulletin of the American Mathematical Society, L’Enseignement Mathématique, Acta Scientiarum Mathematicarum, entre otras, así como de las organizaciones American Mathematical Society, Mathematical Association of America, Association for Symbolic Logic, The Turing Digital Archive, Det Norske Videnskaps-Akademi, Norsk matematisk forening, Unione Matematica Italiana, entre otras.
Conclusión
Si entendemos el acto de divulgar algo meramente como el acto de poner ese algo al alcance del público, entonces hay cierta verdad en que hay al menos dos tipos de divulgación científica: aquella que pretende hacer accesible el conocimiento científico para la comunidad no-científica y aquella que pretende poner al alcance, de la propia comunidad científica, algún conocimiento científico.[6] Estrictamente, la labor de La Reina de las Ciencias no es divulgativa en ninguno de estos dos sentidos, pues 1) no pretende hacer más inteligible el contenido de las obras traducidas ahí publicadas y 2) no está (exclusivamente) dirigida a la comunidad científica. Pero importa poco el nombre que le demos a la labor que, desde el ILCE y su Biblioteca Digital, hacemos con La Reina de las Ciencias. Llámesele como quiera llamársele, nuestro propósito no es otro que el de intentar universalizar los contenidos de la que es, considerada por muchos, la más sublime de las ciencias: las matemáticas.
Referencias
Bell, E. T. (2014). Historia de las matemáticas. FCE.
Organización de las Naciones Unidas. (2015). Percentage of children and adolescents not achieving minimum proficiency in reading and mathematics, en Ensure inclusive and equitable quality education and promote lifelong learning opportunities for all. https://unstats.un.org/sdgs/report/2019/goal-04/
Poincaré, H. (1914). Definiciones matemáticas y educación, en Ciencia y Método. Edición digital para la Biblioteca Digital del ILCE. http://bibliotecadigital.ilce.edu.mx/Colecciones/ReinaCiencias/_docs/Ciencia_y_metodo-Poincare.pdf
Ficha del autor
Emilio Méndez Pinto: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Creador de la colección La Reina de las Ciencias y traductor de las obras contenidas en ella. Actualmente, estudiante de la maestría en filosofía en la Universidad Nacional Autónoma de México. (http://bibliotecadigital.ilce.edu.mx/Colecciones/index.php?clave=ReinaCiencias)
[2] Disponibles en: https://unstats.un.org/sdgs/report/2019/goal-04/.
[3] Entendiendo “obras clásicas” como obras atemporales.
[4] Con una segunda parte: “y la teoría de números es la reina de las matemáticas”. Algunos historiadores de las matemáticas, como Bell, han puesto en duda la atribución a Gauss de esta y otras frases. Al respecto, véase Bell, Eric T. (2014). Historia de las matemáticas. México: FCE.
[5] Además de 18 textos de la autoría del creador y traductor Emilio Méndez Pinto.
[6] Dado el carácter intrínsecamente público del quehacer científico, a este segundo tipo de acto bien podríamos llamarlo, simplemente, hacer ciencia.



